关于三角函数有如下公式: ,
,
利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值.
如:
根据上面的知识,你可以选择适当的公式解决下面问题:
如图,两座建筑物 和 的水平距离 为24米,从点 测得点 的俯角 ,测得点 的俯角 ,求建筑物 的高度.

如图,已知O是直线AB上的一点,OD是∠AOC的平分线,OE是∠COB平分线,求∠DOE的度数.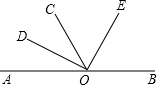
如图,已知∠AOC=∠BOD=75°,∠BOC=30°,求∠AOD.
(1)如图所示,∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数.
(2)如果(1)中∠AOB=α,其他条件不变,求∠MON的度数.
(3)如果(1)中∠BOC=β(β为锐角),其他条件不变,求∠MON的度数.
(4)从(1)(2)(3)的结果你能看出什么规律?
(5)线段的计算与角的计算存在着紧密的联系,它们之间可以互相借鉴解法,请你模仿(1)~(4),设计一道以线段为背景的计算题,并写出其中的规律来?
如图,将一幅角板的直角顶点叠放在一起.
(1)猜想∠AOC与∠BOD的大小关系,并说明理由;
(2)求∠AOD+∠BOC的度数;
(3)若∠BOD:∠AOD=2:11,求∠BOC的度数.
如图,∠AOB=90°,∠AOC为锐角,且ON平分∠AOC,射线OM在∠BON内部.
(1)请你数一数,图中共有多少个小于平角的角.
(2)如果∠AOC=50°,∠MON=45°.
①求∠AOM的度数;
②请通过计算说明OM是否平分∠BOC.
(3)如果∠AOC=x°,∠MON=45°,OM是否平分∠BOC?请说明理由.