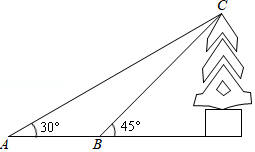
在数学实践活动课上，老师带领同学们到附近的湿地公园测量园内雕塑的高度．用测角仪在 处测得雕塑顶端点 的仰角为 ，再往雕塑方向前进4米至 处，测得仰角为 ．问：该雕塑有多高？（测角仪高度忽略不计，结果不取近似值．
如图，已知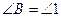
，
是△
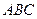的角平分线，求证：
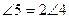.请在下面横线上填出推理的依据：
证明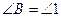：∵ ，（已知）
∴ 
∥
．（同位角相等、两直线平行）
∴ 
．（）
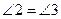∵ 是△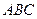的角平分线，（）
∴ 
．（）
∴ 
．（）
∵ 
，（三角形的一个外角等于与它不相邻的两个内角和）
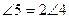∴ ．（等量代换）
如图，若AB∥CD，EF与AB 、CD分别相交于E、
F，EP⊥EF，∠EFD的平分线与EP相交于点P，且∠BEP=40°，求∠EFP的度数.
如图，一艘轮船在A处看见巡逻艇M在其北偏东62°的方向上，此时一艘客船在B处看见巡逻艇M在其北偏东13°的方向上，试求此时从巡逻艇上看这两艘船的视角∠AMB的度数。
如图2，已知AB∥CD，直线EF分别交AB、CD于点E、F，EG平分∠BEF，若∠1=50°，求∠2的度数。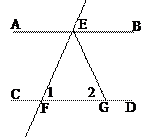
已知，如图，在△
中，
于
，若
54°，试求
的度数.
．