为了提高学生的身体素质，某班级决定开展球类活动，要求每个学生必须在篮球、足球、排球、乒乓球、羽毛球中选择一项参加训练（只选择一项），根据学生的报名情况制成如下统计表：
项目 |
篮球 |
足球 |
排球 |
乒乓球 |
羽毛球 |
报名人数 |
12 |
8 |
4 |
|
10 |
占总人数的百分比 |
|
|
（1）该班学生的总人数为 人；
（2）由表中的数据可知： ， ；
（3）报名参加排球训练的四个人为两男（分别记为 、 两女（分别记为 、 ，现要随机在这4人中选2人参加学校组织的校级训练，请用列表或树状图的方法求出刚好选中一男一女的概率．
如图，已知△ABC．按如下步骤作图：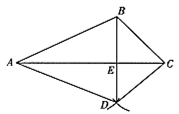
①以A为圆心，AB长为半径画弧；
②以C为圆心，CB长为半径画弧,两弧相交于点D；
③连结BD，与AC交于点E，连结AD，CD．
（1）求证：△ABC≌△ADC；
（2）若∠BAC =30°,∠BCA = 45°,AC = 4，求BE的长．
在Rt△ABC中，∠A=90°，AC=AB=4， D，E分别是AB，AC的中点．若等腰Rt△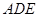
绕点A逆时针旋转，得到等腰Rt△
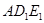，设旋转角为
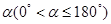，记直线
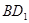与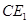
的交点为P．
（1）如图1，当
时，线段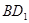的长等于 ，线段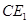的长等于 ；（直接填写结果）
（2）如图2，当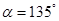
时，求证：
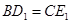,且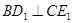
；
（3）①设BC的中点为M，则线段PM的长为 ；②点P到AB所在直线的距离的最大值为 ．（直接填写结果）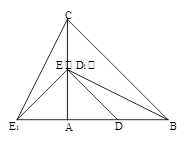
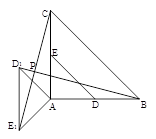
如图，已知△ABC．按如下步骤作图：①以A为圆心，AB长为半径画弧；②以C为圆心，CB长为半径画弧，两弧相交于点D；③连结BD，与AC交于点E，连结AD，CD．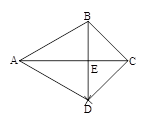
（1）求证：△ABC≌△ADC；
（2）若∠BAC=30°，∠BCA=45°，AC=4，求BE的长．
小丽为了测旗杆AB的高度，小丽眼睛距地图1．5米，小丽站在C点，测出旗杆A的仰角为30o，小丽向前走了10米到达点E，此时的仰角为60o，求旗杆的高度。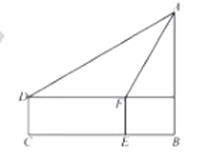
如图，在同一平面上，两块斜边相等的直角三角板Rt△ABC与Rt△ADC拼在一起，使斜边AC完全重合，且顶点B，D分别在AC的两旁，∠ABC=∠ADC=90°，∠CAD=30°，AB=BC=4cm．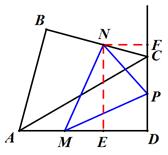
（1）填空：AD= （cm），DC= （cm）；
（2）点M，N分别从A点，C点同时以每秒1cm的速度等速出发，且分别在AD，CB上沿A→D，C→B的方向运动，当N点运动 到B点时，M，N两点同时停止运动，连结MN，求当M，N点运动了x秒时，点N到AD的距离（用含x的式子表示）；
（3）在（2）的条件下，取DC中点P，连结MP，NP，设△PMN的面积为y（cm2），在整个运动过程中，△PMN的面积y存在最大值，请求出这个最大值．
（参考数据：sin75°=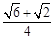
，sin15°=
）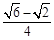