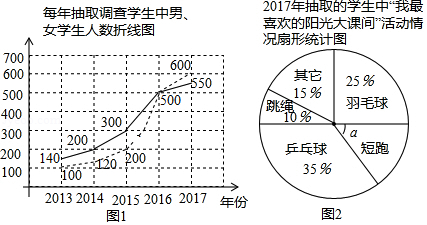
西昌市教科知局从2013年起每年对全市所有中学生进行“我最喜欢的阳光大课间活动”抽样调查(被调查学生每人只能选一项),并将抽样调查的数据绘制成图1、图2两幅统计图,根据统计图提供的信息解答下列问题:
(1) 年抽取的调查人数最少; 年抽取的调查人数中男生、女生人数相等;
(2)求图2中“短跑”在扇形图中所占的圆心角 的度数;
(3)2017年抽取的学生中,喜欢羽毛球和短跑的学生共有多少人?
(4)如果2017年全市共有3.4万名中学生,请你估计我市2017年喜欢乒乓球和羽毛球两项运动的大约有多少人?
两个直角边为6的全等的等腰直角三角形Rt△AOB和Rt△CED,按如图一所示的位置放置,点O与E重合.
(1)Rt△AOB固定不动,Rt△CED沿x轴以每秒2个单位长度的速度向右运动,当点E运动到与点B重合时停止,设运动x秒后,Rt△AOB和Rt△CED的重叠部分面积为y,求y与x之间的函数关系式;
(2)当Rt△CED以(1)中的速度和方向运动,运动时间x=2秒时,Rt△CED运动到如图二所示的位置,若抛物线y=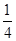 x2+bx+c过点A,G,求抛物线的解析式;
x2+bx+c过点A,G,求抛物线的解析式;
(3)现有一动点P在(2)中的抛物线上运动,试问点P在运动过程中是否存在点P到x轴或y轴的距离为2的情况?若存在,请求出点P的坐标;若不存在,请说明理由.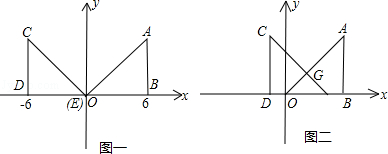
如图,已知直线AB与x轴、y轴分别交于A和B,OA=4,且OA、OB长是关于x的方程x2﹣mx+12=0的两实根,以OB为直径的⊙M与AB交于C,连接CM并延长交x轴于N.
(1)求⊙M的半径.
(2)求线段AC的长.
(3)若D为OA的中点,求证:CD是⊙M的切线.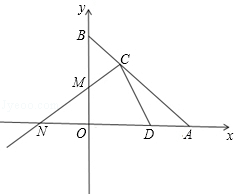
某商店销售一种商品,每件的进价为2.5元,根据市场调查,销售量与销售单价满足如下关系:在一段时间内,单价是13.5元时,销售量为500件,而单价每降低1元,就可以多售出200件.请你分析,销售单价多少时,可以获利最大?
已知:如图一次函数y= x﹣3的图象与x轴、y轴分别交于A、B两点,过点C(4,0)作AB的垂线交AB于点E,交y轴于点D,求点D、E的坐标.
x﹣3的图象与x轴、y轴分别交于A、B两点,过点C(4,0)作AB的垂线交AB于点E,交y轴于点D,求点D、E的坐标.
甲、乙两条轮船同时从港口A出发,甲轮船以每小时30海里的速度沿着北偏东60°的方向航行,乙轮船以每小时15海里的速度沿着正东方向行进,1小时后,甲船接到命令要与乙船会合,于是甲船改变了行进的速度,沿着东南方向航行,结果在小岛C处与乙船相遇.假设乙船的速度和航向保持不变,求:
(1)港口A与小岛C之间的距离;
(2)甲轮船后来的速度.