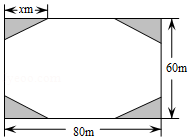
结合西昌市创建文明城市要求,某小区业主委员会决定把一块长 ,宽 的矩形空地建成花园小广场,设计方案如图所示,阴影区域为绿化区(四块绿化区为全等的直角三角形),空白区域为活动区,且四周出口宽度一样,其宽度不小于 ,不大于 ,预计活动区造价60元 ,绿化区造价50元 ,设绿化区域较长直角边为 .
(1)用含 的代数式表示出口的宽度;
(2)求工程总造价 与 的函数关系式,并直接写出 的取值范围;
(3)如果业主委员会投资28.4万元,能否完成全部工程?若能,请写出 为整数的所有工程方案;若不能,请说明理由.
(4)业主委员会决定在(3)设计的方案中,按最省钱的一种方案,先对四个绿化区域进行绿化,在实际施工中,每天比原计划多绿化 ,结果提前4天完成四个区域的绿化任务,问原计划每天绿化多少 .
在平面直角坐标系xOy中,二次函数 的图象经过(
的图象经过( ,0)和(
,0)和( ,0)两点.
,0)两点.
(1)求此二次函数的表达式.
(2)直接写出当 <x<1时,y的取值范围.
<x<1时,y的取值范围.
(3)将一次函数 y=(1-m)x+2的图象向下平移m个单位后,与二次函数 图象交点的横坐标分别是a和b,其中a<2<b,试求m的取值范围.
图象交点的横坐标分别是a和b,其中a<2<b,试求m的取值范围.
如图,定义:在Rt△ABC中,∠C =90°,锐角α的邻边与对边的比叫做角α的余切,记作ctanα,即ctanα=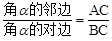 .
.
根据上述角的余切定义,解答下列问题:
(1)ctan60°=.
(2)求ctan15°的值.
如图, Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E为BC边的中点,连接DE.
(1)求证:DE与⊙O 相切.
(2)若tanC= ,DE=2,求AD的长.
,DE=2,求AD的长.
学生的上学方式是初中生生活自理能力的一种反映.为此,怀柔区某初三数学老师组织本班学生,运用他们所学的统计知识,对初一学生上学的四种方式:骑车、步行、乘车、接送,进行抽样调查,并将调查的结果绘制成图(1)、图(2).请根据图中提供的信息,解答下列问题:
(1)抽样调查的样本容量为________,其中步行人数占样本容量的_____%,骑车人数占样本容量的_____%.
(2)请将图(1)补充完整.
(3)根据抽样调查结果,你估计该校初一年级800名学生中,大约有多少名学生是由家长接送上学的?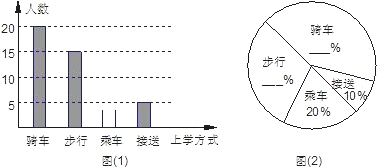
如图,在平行四边形ABCD中,∠ABC=45°,E、F分别在CD和BC的延长线上,AE∥BD,∠EFC=30°, AB=2.
求CF的长.