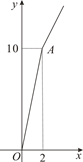如果将四根木条首尾相连，在相连处用螺钉连接，就能构成一个平面图形．
（1）若固定三根木条 ， ， 不动， ， ，如图，量得第四根木条 ，判断此时 与 是否相等，并说明理由．
（2）若固定二根木条 、 不动， ， ，量得木条 ， ，写出木条 的长度可能取得的一个值（直接写出一个即可）
（3）若固定一根木条 不动， ，量得木条 ，如果木条 ， 的长度不变，当点 移到 的延长线上时，点 也在 的延长线上；当点 移到 的延长线上时，点 、 、 能构成周长为 的三角形，求出木条 ， 的长度．
已知：抛物线y=
+（2m－1）x+
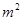－1经过坐标原点，且当x＜0时，y随x的增大而减小．
（1）求抛物线的解析式，并写出y＜0时，对应x的取值范围;
（2）设点A是该抛物线上位于x轴下方的一个动点，过点A作x轴的平行线交抛物线于另一点D，再作AB⊥x轴于点B， DC⊥x轴于点C．
①当BC=1时，直接写出矩形ABCD的周长;
②设动点A的坐标为 （a，b），将矩形ABCD的周长L表示为a的函数并写出自变量的取值范围，判断周长是否存在最大值，如果存在，求出这个最大值，并求出此时点A的坐标;如果不存在，请说明理由．
如图，⊙O是△ABC的外接圆，P是⊙O外的一点，AM是⊙O的直径，∠PAC=∠ABC
（1） 求证：PA是⊙O的切线；
（2） 连接PB与AC交于点D，与⊙O交于点E，F为BD上的一点，若M为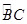
的中点，且∠DCF=∠P，求证：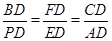
如图，在平面直角坐标系中A点的坐标为（8，y） ，AB⊥x轴于点B, sin∠OAB=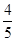
，反比例函数y=
的图象的一支经过AO的中点C，且与AB交于点D．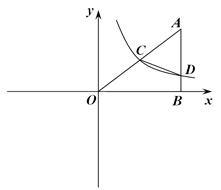
（1）求反比例函数解析式;
（2）若函数y="3x" 与y=的图象的另一支交于点M，求三角形OMB与四边形OCDB的面积的比．
学校准备从甲乙两位选手中选择一位选手代表学校参加所在地区的汉字听写大赛，学校对两位选手从表达能力、阅读理解、综合素质和汉字听写四个方面做了测试，他们各自的成绩（百分制）如下表:
| 选手 |
表达能力 |
阅读理解 |
综合素质 |
汉字听写 |
| 甲 |
85 |
78 |
85 |
73 |
| 乙 |
73 |
80 |
82 |
83 |
（1）由表中成绩已算得甲的平均成绩为80．25，请计算乙的平均成绩，从他们的这一成绩看，应选派谁;
（2）如果表达能力、阅读理解、综合素质和汉字听写分别赋予它们2、1、3和4的权，请分别计算两名选手的平均成绩，从他们的这一成绩看，应选派谁．[来
某玉米种子的价格为a元/千克，如果一次购买2千克以上的种子，超过2千克部分的种子价格打8折．某科技人员对付款金额和购买量这两个变量的对应关系用列表法做了分析，并绘制出了函数图象．以下是该科技人员绘制的图象和表格的不完整资料，已知点A的坐标为（2，10）．请你结合表格和图象：
| 付款金额（元） |
a |
7．5 |
10 |
12 |
b |
| 购买量（千克） |
1 |
1．5 |
2 |
2．5 |
3 |
（1）指出付款金额和购买量哪个变量是函数的自变量x，并写出表中a、b的值；
（2）求出当x＞2时，y关于x的函数解析式；
（3）甲农户将8．8元钱全部用于购买该玉米种子，乙农户购买了4165克该玉米种子，分别计算他们的购买量和付款金额．