为深化义务教育课程改革，某校积极开展拓展性课程建设，计划开设艺术、体育、劳技、文学等多个类别的拓展性课程，要求每一位学生都自主选择一个类别的拓展性课程．为了了解学生选择拓展性课程的情况，随机抽取了部分学生进行调查，并将调查结果绘制成如下统计图（部分信息未给出）
根据统计图中的信息，解答下列问题：
（1）求本次被调查的学生人数．
（2）将条形统计图补充完整．
（3）若该校共有1600名学生，请估计全校选择体育类的学生人数．
有四张背面相同的纸牌A，B，C，D，其正面分别画有四个不同的几何图形（如图）．小华将这4张纸牌背面朝上洗匀后摸出一张，放回洗匀后再摸出一张．用树状图(或列表法)表示两次摸牌所有可能出现的结果（纸牌可用A，B，C，D表示）；
求摸出两张牌面图形都是中心对称图形的纸牌的概率．
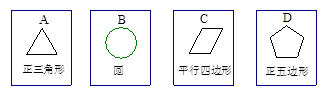
先化简，再求值：
，其中x＝－4．
解不等式组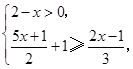
并把解集在数轴上表示出来。
计算：
．
两个全等的直角三角形ABC和DEF重叠在一起，其中AB=2，AC=1．．固定△ABC不动，将△DEF进行如下操作：如图（1），△DEF沿线段AB向右平移（即D点在线段AB内移动），连结DC、CF、FB，四边形CDBF的形状在不断的变化，它的面积是否变化，如果不变请求出其面积．如果变化，说明理由．
如图（2），当D点移到AB的中点时，请你猜想四边形CDBF的形状，并说明理由．
