如图，已知： 是 的直径，点 在 上， 是 的切线， 于点 ， 是 延长线上一点， 交 于点 ，连接 、 ．
（1）求证： 平分 ．
（2）若 ，
①求 的度数；
②若 的半径为 ，求线段 的长．
如图，小明家在A处，门前有一口池塘，隔着池塘有一条公路l，AB是A到l的小路. 现新修一条路AC到公路l. 小明测量出∠ACD=30º，∠ABD=45º，BC=50m. 请你帮小明计算他家到公路l的距离AD的长度（精确到0.1m；参考数据：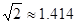
，
）.
一个口袋中有4个小球，这4个小球分别标记为1，2，3，4．
（1）随机模取一个小球，求恰好模到标号为2的小球的概率；
（2）随机模取一个小球然后放回，再随机模取一个小球，求两次模取的小球的标号的和为3的概率．
如图，已知一次函数与反比例函数的图象交于点P（-2，-1）和点Q（1，m）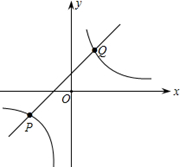
（1）求这两个函数的关系式；
（2）根据图象，直接写出当一次函数的值大于反比例函数的值时自变量x的取值范围．
（1）计算：
；（2）解方程：
．
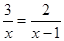已知：把Rt△ABC和Rt△DEF按如图（1）摆放（点C与点E重合），点B、C（E）、F在同一条直线上．∠ACB = ∠EDF = 90°，∠DEF = 45°，AC =6
cm，BC =" 6" cm，EF = 12cm．
如图（2），△DEF从图（1）的位置出发，以1 cm/s的速度沿CB向△ABC匀速移动，在△DEF移动的同时，点P从△ABC的顶点B出发，以2 cm/s的速度沿BA向点A匀速移动.当△DEF的顶点D移动到AC边上时，△DEF停止移动，点P也随之停止移动．DE与AC相交于点Q，连接PQ，设移动时间为t（s）
．解答下列问题：
（1）当t为何值时，点A在线段PQ的垂直平分线上？
（2）当t为何值时，△PQE是直角三角形？
（3）连接PE，设四边形APEC的面积为y（cm2），求y与t之间的函数关系式；是否存在某一时刻t，使面积y最小？若存在，求出y的最小值；若不存在，说明理由．
（4）是否存在某一时刻t，使P、Q、F三点在同一条直线上？若存在，求出此时t的值；若不存在，说明理由