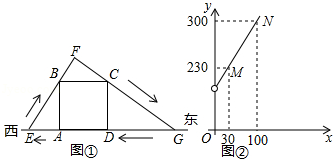
如图①,直线 表示一条东西走向的笔直公路,四边形 是一块边长为100米的正方形草地,点 , 在直线 上,小明从点 出发,沿公路 向西走了若干米后到达点 处,然后转身沿射线 方向走到点 处,接着又改变方向沿射线 方向走到公路 上的点 处,最后沿公路 回到点 处.设 米(其中 , 米,已知 与 之间的函数关系如图②所示,
(1)求图②中线段 所在直线的函数表达式;
(2)试问小明从起点 出发直至最后回到点 处,所走过的路径(即 是否可以是一个等腰三角形?如果可以,求出相应 的值;如果不可以,说明理由.
已知关于 的一元二次方程x2+2x+2k-4=0
的一元二次方程x2+2x+2k-4=0 有两个不相等的实数根。
有两个不相等的实数根。
(1)求 的取值范围;
的取值范围;
(2)若k为正整数,且该方程的根都是整数,求 的值。
的值。
(1)解不等式组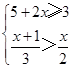 ,并写出不等式组的整数解.
,并写出不等式组的整数解.
(2)某园林队计划由6名工人对180平方米的区域进行绿化,由于施工时增加了2名工人,结果比计划提前3小时完成任务。若每人每小时绿化面积相同,求每人每小时的绿化面积。
(1)计算: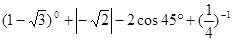 ;
;
(2)先化简,再求值: ,其中x是方程
,其中x是方程 的根.
的根.
阅读下列解题过程: ;
;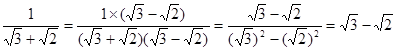 .
.
利用上面所提供的解法,化简 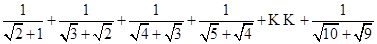
(2)观察上面的解题过程,请直接写出: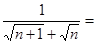 。(n为正整数)
。(n为正整数)
已知:如图,正方形ABCD中,P是对角线BD上的一个动点,PE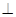 CD于E, PF
CD于E, PF BC于F,连接EF,求证:AP=EF.
BC于F,连接EF,求证:AP=EF.