如图, 、 分别是 的直径和弦, 于点 .过点 作 的切线与 的延长线交于点 , 、 的延长线交于点 .
(1)求证: 是 的切线;
(2)若 , ,求线段 的长.

如图,正方形网格中,△ABC为格点三角形(顶点都是格点),将△ABC绕点A按逆时针方向旋转90°得到△AB1C1.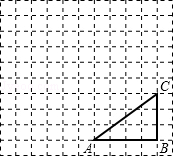
(1)在正方形网格中,作出△AB1C1;(不要求写作法)
(2)设网格小正方形的边长为1cm,用阴影表示出旋转过程中线段BC所扫过的图形,然后求出它的面积.(结果保留π).
在1个不透明的口袋里,装有红、白、黄三种颜色的乒乓球(除颜色外,其余都相同),其中有白球2个,黄球1个,若从中任意摸出一个球,这个球是白色的概率为0.5.
(1)求口袋中红球的个数;
(2)若摸到红球记0分,摸到白球记1分,摸到黄球记2分,甲从口袋中摸出一个球,不放回,再找出一个画树状图的方法求甲摸的两个球且得2分的概率.
(1)计算:(2 ﹣
﹣ )÷
)÷ +2
+2 (2)解方程:2x2﹣x﹣1=0.
(2)解方程:2x2﹣x﹣1=0.
学校计划用地面砖铺设教学楼前矩形广场的地面ABCD,已知矩形广场地面的长为100米,宽为80米.图案设计如图所示:广场的四角为小正方形,阴影部分为四个矩形,四个矩形的宽都为小正方形的边长,阴影部分铺绿色地面砖,其余部分铺白色地面砖.
(1)要使铺白色地面砖的面积为5200平方米,那么矩形广场四角的小正方形的边长为多少米?
(2)如果铺白色地面砖的费用为每平方米30元.铺绿色地面砖的费用为每平方米20元,当广场四角小正方形的边长为多少米时,铺广场地面的总费用最少?最少费用是多少?
某教室的开关控制板上有四个外形完全相同的开关,其中两个分别控制A、B两盏电灯,另两个分别控制C、D两个吊扇.已知电灯、吊扇均正常,且处于不工作状态,开关与电灯、电扇的对应关系未知.
(1)若四个开关均正常,则任意按下一个开关,正好一盏灯亮的概率是多少?
(2)若其中一个控制电灯的开关坏了,则任意按下两个开关,正好一盏灯亮和一个扇转的概率是多少?请用树状图法或列表法加以说明.