如图,将等腰直角三角形纸片 对折,折痕为 .展平后,再将点 折叠在边 上(不与 、 重合),折痕为 ,点 在 上的对应点为 ,设 与 交于点 ,连接 .已知 .
(1)若 为 的中点,求 的长;
(2)随着点 在边 上取不同的位置,
① 的形状是否发生变化?请说明理由;
②求 的周长的取值范围.

解方程:(本题共2小题,每题4分,共8分)
(1)  (2)1-
(2)1- =
= .
.
分解分式: .
.
计算: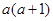 .
.
如图,已知在△ABC中,∠ACB=90°,CD⊥AB,D为垂足.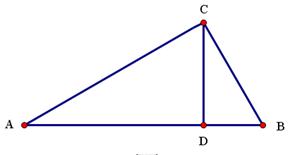
(1)若AC=8,BC=6求AB和AD的长;
(2)设AB=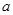 ,CD=
,CD=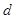 ,AC=
,AC=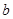 ,BC=
,BC=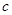 ,试说明:
,试说明: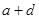 >
>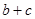 .
.
图1是一个长为2 ,宽为2
,宽为2 的长方形,沿图中虚线剪开,可分成四块小长方形.
的长方形,沿图中虚线剪开,可分成四块小长方形.
(1)求出图1的长方形面积;
(2)将四块小长方形拼成一个图2的正方形.利用阴影部分面积的不同表示方法,直接写出代数式( )2、(
)2、( )2、
)2、 之间的等量关系;
之间的等量关系;
(3)把四块小长方形不重叠地放在一个长方形的内部(如图3),未被覆盖的部分用
阴影表示.求两块阴影部分的周长和(用含 、
、 的代数式表示).
的代数式表示).