综合与实践
问题情境:
如图①,点 为正方形 内一点, ,将 绕点 按顺时针方向旋转 ,得到 (点 的对应点为点 .延长 交 于点 ,连接 .
猜想证明:
(1)试判断四边形 的形状,并说明理由;
(2)如图②,若 ,请猜想线段 与 的数量关系并加以证明;
解决问题:
(3)如图①,若 , ,请直接写出 的长.

如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D。
试说明:AC∥DF。
解:因为 ∠1=∠2(已知)
∠1=∠3,∠2=∠4()
所以∠3=∠4(等量代换)
所以 ∥()
所以 ∠C=∠ABD,()
又因为 ∠C=∠D(已知)
所以∠D=∠ABD(等量代换)
所以 AC∥DF()
如图,已知直线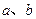 被直线
被直线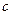 所截,
所截,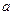 ∥
∥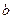 ,如果
,如果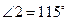 ,求∠1的度数。
,求∠1的度数。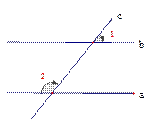
已知:如图,在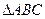 中,
中,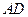 是
是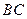 边上的高,
边上的高, 是
是 平分线.
平分线.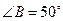 ,
,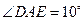 。
。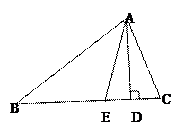
(1)求 的度数;
的度数;
(2)求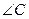 的度数.
的度数.
如图,△ABC中,BD是∠ABC的平分线,DE∥BC交AB于E,∠A=60°,
∠BDC=100°求∠BDE的度数。
如图,直线CD与直线AB相交于C,根据下列语句画图、解答。
(1)过点P作PQ∥CD,交AB于点Q
(2)过点P作PR⊥CD,垂足为R
(3)若∠DCB=1200,猜想∠PQC是多少度?并说明理由