列方程(组 解应用题
某驻村工作队,为带动群众增收致富,巩固脱贫攻坚成效,决定在该村山脚下,围一块面积为 的矩形试验茶园,便于成功后大面积推广.如图所示,茶园一面靠墙,墙长 ,另外三面用 长的篱笆围成,其中一边开有一扇 宽的门(不包括篱笆).求这个茶园的长和宽.

在甲村至乙村的公路有一块山地正在开发,现有一C处需要爆破.已知点C与公路上的停靠站A的距离为300米,与公路上的另一停靠站B的距离为400米,且CA⊥CB,如图所示.为了安全起见,爆破点C周围半径250米范围内不得进入,问在进行爆破时,公路AB段是否有危险而需要暂时封锁? 请通过计算进行说明.
如图,李老师设计了一个探究杠杆平衡条件的实验:在一个自制类似天平的仪器的左边固定托盘A中放置一个重物,在右边的活动托盘B(可左右移动)中放置一定质量的砝码,使得仪器左右平衡,改变活动托盘B与点O的距离x(cm),观察活动托盘B中砝码的质量y(g)的变化情况.实验数据记录如下表:
(1)把上表中(x,y)的各组对应值作为点的坐标,在坐标系中描出相应的点,用平滑曲线连接这些点;
(2)观察所画的图象,猜测y与x之间的函数关系,求出函数关系式并加以验证.
已知:如图,AB⊥AC,垂足为点A,AB=3,AC=4,BD=12,CD=13.
(1)求BC的长;(2)证明:BC⊥BD.
解方程:
(1)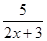 =
=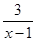 ;
;
(2)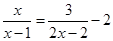
计算:
(1)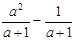 ;
;
(2)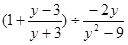 .
.