如图所示，AB是⊙O的直径，AD和BC分别切⊙O于A，B两点-优题课

题文

如图所示， $AB$ 是 $⊙ O$ 的直径， $AD$ 和 $BC$ 分别切 $⊙ O$ 于 $A$ ， $B$ 两点， $CD$ 与 $⊙ O$ 有公共点 $E$ ，且 $AD = DE$ ．

（1）求证： $CD$ 是 $⊙ O$ 的切线；

（2）若 $AB = 12$ ， $BC = 4$ ，求 $AD$ 的长．

科目数学题型解答题难度中等

知识点：圆周角定理全等三角形的判定与性质矩形的判定与性质切线的判定与性质勾股定理

相关试题

某商店营业员每月的基本工资为800元，奖金制度是：每月完成规定指标10000元营业额的，发奖金300元；若营业额超过规定指标，另奖超额部分营业额的5%，该商店的一名营业员九月份完成营业额15000元，问他九月份的收入为多少元？

若，求代数式的值．

已知，求代数式的值．

在一次“手拉手”捐款活动中，某同学对甲．乙两班捐款的情况进行统计，得到如下三条信息：
信息一．甲班共捐款120元，乙班共捐款88元；
信息二．乙班平均每人捐款数是甲班平均每人捐款数的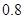倍；
信息三．甲班比乙班多5人。
请你根据以上三条信息，求出甲班平均每人捐款多少元？

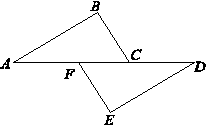
如图，点A、F、C、D在同一直线上，点B和点E分别在直线AD的两侧，且AB＝DE，∠A＝∠D，AF＝DC．求证：BC∥EF．