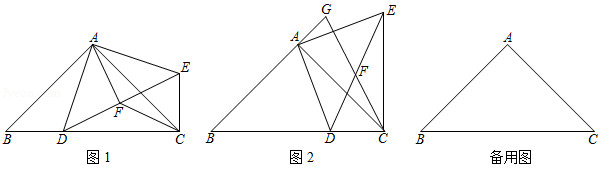
如图,在 中, , ,点 是 边上一动点,连接 ,把 绕点 逆时针旋转 ,得到 ,连接 , .点 是 的中点,连接 .
(1)求证: ;
(2)如图2所示,在点 运动的过程中,当 时,分别延长 , ,相交于点 ,猜想 与 存在的数量关系,并证明你猜想的结论;
(3)在点 运动的过程中,在线段 上存在一点 ,使 的值最小.当 的值取得最小值时, 的长为 ,请直接用含 的式子表示 的长.
甲乙两运输队,甲队原有32人,乙队原有28人,若从乙队调走一些人到甲队,那么甲队人数恰好是乙队人数的2倍,问从乙队调走了多少人到甲队?
已知点A、B、C在同一条直线上,AB=10cm,BC=4cm,若M是AC的中点,求线段BM的长度.
某检修站,工人乘一辆汽车沿东西方向的公路检修线路,约定向东为正,向西为负,从A地出发到收工时,行走记录为(单位:千米):
15,-2,+5,-1,+10,-3,-2,+12,+4,-5,+6
计算收工时,工人在A地的哪一边,距A地多远?
如图,O是直线AB上一点,OD平分∠BOC,∠COE=90°. 若∠AOC=40°,求∠DOE的度数。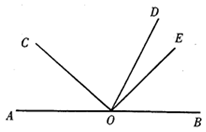
如图,平面内有A,B,C,D四点,按下列语句画图:
(1)、画直线AB,射线BC,线段BD;(2)、连接AD与BC相交于点E.