如图，在平面直角坐标系中，已知二次函数y12(xm)24图象-优题课

如图，在平面直角坐标系中，已知二次函数 $y = - \frac{1}{2} {(x - m)}^{2} + 4$ 图象的顶点为 $A$ ，与 $y$ 轴交于点 $B$ ，异于顶点 $A$ 的点 $C (1, n)$ 在该函数图象上．

（1）当 $m = 5$ 时，求 $n$ 的值．

（2）当 $n = 2$ 时，若点 $A$ 在第一象限内，结合图象，求当 $y ⩾ 2$ 时，自变量 $x$ 的取值范围．

（3）作直线 $AC$ 与 $y$ 轴相交于点 $D$ ．当点 $B$ 在 $x$ 轴上方，且在线段 $OD$ 上时，求 $m$ 的取值范围．

科目数学题型解答题难度中等

知识点：二次函数的性质待定系数法求二次函数解析式二次函数综合题

如图，已知锐角 $ΔABC$ 中， $AC = BC$ ．

（1）请在图1中用无刻度的直尺和圆规作图：作 $∠ ACB$ 的平分线 $CD$ ；作 $ΔABC$ 的外接圆 $⊙ O$ ；（不写作法，保留作图痕迹）

（2）在（1）的条件下，若 $AB = \frac{48}{5}$ ， $⊙ O$ 的半径为5，则 $\sin B =$ 　　．（如需画草图，请使用图 $2)$

某企业为推进全民健身活动，提升员工身体素质，号召员工开展健身锻炼活动，经过两个月的宣传发动，员工健身锻炼的意识有了显著提高．为了调查本企业员工上月参加健身锻炼的情况，现从1500名员工中随机抽取200人调查每人上月健身锻炼的次数，并把调查所得的数据整理如下：

某企业员工参加健身锻炼次数的频数分布表

锻炼次数 $x$ （代号）

$0 < x ⩽ 5$

（A）

$5 < x ⩽ 10$

（B）

$10 < x ⩽ 15$

（C）

$15 < x ⩽ 20$

（D）

$20 < x ⩽ 25$

（E）

$25 < x ⩽ 30$

$(F)$

频数

$a$

$c$

频率

0.05

$b$

0.34

$d$

0.12

0.03

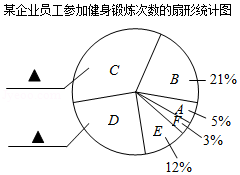
（1）表格中 $a =$ 　　；

（2）请把扇形统计图补充完整；（只需标注相应的数据）

（3）请估计该企业上月参加健身锻炼超过10次的员工有多少人？

把4张分别写有数字1、2、3、4的卡片（卡片的形状、大小、质地都相同）放在盒子中，搅匀后从中任意取出1张卡片，记录后放回、搅匀，再从中任意取出1张卡片．求下列事件发生的概率．（请用“画树状图”或“列表”等方法写出分析过程）

（1）取出的2张卡片数字相同；

（2）取出的2张卡片中，至少有1张卡片的数字为“3”．

已知：如图， $AC$ ， $DB$ 相交于点 $O$ ， $AB = DC$ ， $∠ ABO = ∠ DCO$ ．

求证：（1） $ΔABO ≅ ΔDCO$ ；

（2） $∠ OBC = ∠ OCB$ ．

计算：

（1） $| - \frac{1}{2} | - {(- 2)}^{3} + \sin 30 °$ ；

（2） $\frac{4}{a} - \frac{a + 8}{2 a}$ ．