如图1,矩形 中, , , 中, , , , 的延长线相交于点 ,且 , , .将 绕点 逆时针旋转 得到△ .
(1)当 时,求点 到直线 的距离.
(2)在图1中,取 的中点 ,连结 ,如图2.
①当 与矩形 的一条边平行时,求点 到直线 的距离.
②当线段 与矩形 的边有且只有一个交点时,求该交点到直线 的距离的取值范围.

作图题
(1)如左图,平移方格纸中的图形,使点A平移到点 A'处,画出平移后的图形。

(2)分析图①、②、④中阴影部分的分布规律,按此规律在图③中画出其中的阴影部分.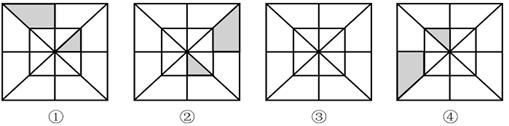
如图,四边形ABCD是一块草坪,量得四边长AB=3m,BC=4m,DC=12m,AD=13m,∠B=90°,求这块草坪的面积。
计算
(1) (2)(
(2)( +
+ )2
)2
(3) (4)
(4)
已知O为直线AB上的一点,∠COE是直角, OF 平分∠AOE.
(1)如图①,若∠COF=34°,则∠BOE=°;若∠COF=m°,则∠BOE=°;由上面的解答可知:∠BOE与∠COF之间的数量关系应该为.
(2)如图②,(1)中∠BOE与∠COF之间的数量关系是否仍然成立?若成立,请给予证明;若不成立,请说明理由.
(3)如图③,在(2)的情况下,若∠COF=65°,在∠BOE的内部是否存在一条射线OD,使得2∠BOD与∠AOF的和等于∠BOE与∠BOD的差的一半?若存在,请求出∠BOD的度数;若不存在,请说明理由.
观察算式:1×3+1=4=22;2×4+1=9=32;3×5+1="16=" 42;4×6+1=25=52,……
(1)请根据你发现的规律填空:6×8+1=
 ;
;
(2)用含n的等式表示上面的规律:;
(3)用找到的规律解决下面的问题:
计算:(1+ )(1+
)(1+ )(1+
)(1+ )(1+
)(1+ )…(1+
)…(1+ )
)