我们把方程 称为圆心为 、半径长为 的圆的标准方程.例如,圆心为 、半径长为3的圆的标准方程是 .在平面直角坐标系中, 与轴交于点 , ,且点 的坐标为 ,与 轴相切于点 ,过点 , , 的抛物线的顶点为 .
(1)求 的标准方程;
(2)试判断直线 与 的位置关系,并说明理由.

某校开展校园“美德少年”评选活动,共有“助人为乐”,“自强自立”、“孝老爱亲”,“诚实守信”四种类别,每位同学只能参评其中一类,评选后,把最终入选的20位校园“美德少年”分类统计,制作了如下统计表,后来发现,统计表中前两行的数据都是正确的,后两行的数据中有一个是错误的.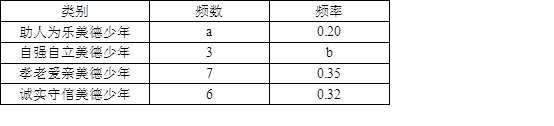
根据以上信息,解答下列问题:
(1)统计表中的a=______,b______;
(2)统计表后两行错误的数据是______,该数据的正确值是______;
(3)校园小记者决定从A,B,C三位“自强自立美德少年”中随机采访两位,用画树状图或列表的方法,求A,B都被采访到的概率.
清明期间,某校师生组成200个小组参加“保护环境,美化家园”植树活动.综合实际情况,校方要求每小组植树量为2至5棵,活动结束后,校方随机抽查了其中50个小组,根据他们的植树量绘制出如图所示的两幅不完整统计图.请根据图中提供的信息,解答下面的问题:
(1)请把条形统计图补充完整,并算出扇形统计图中,植树量为“5棵树”的圆心角是 °.
(2)请你帮学校估算此次活动共种多少棵树.
为弘扬 “东亚文化”,某单位开展了“东亚文化之都”演讲比赛,在安排1位女选手和3位男选手的出场顺序时,采用随机抽签方式.
(1)请直接写出第一位出场是女选手的概率;
(2)请你用画树状图或列表的方法表示第一、二位出场选手的所有等可能结果,并求出他们都是男选手的概率.
为建设”书香校园“,某校开展读书月活动,现随机抽取了一部分学生的日人均阅读时间x(单位:小时)进行统计,统计结果分为四个等级,分别记为A,B,C,D,其中:A:0≤x<0.5,B:0.5≤x<1,C:1≤x<1.5,D:1.5≤x<2,根据统计结果绘制了如图两个尚不完整的统计图.
(1)本次统计共随机抽取了 名学生;
(2)扇形统计图中等级B所占的圆心角是 ;
(3)从参加统计的学生中,随机抽取一个人,则抽到“日人均阅读时间大于或等于1小时”的学生的概率是 ;
(4)若该校有1200名学生,请估计“日人均阅读时间大于或等于0.5小时”的学生共有 人.
某商场经理对某一品牌旅游鞋近一个月的销售情况进行统计后,绘制了如下统计表与条形图: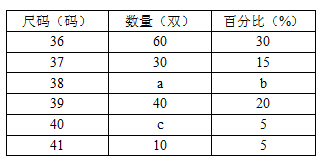
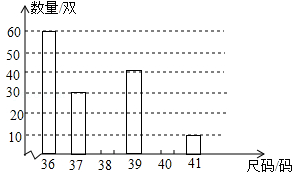
(1)写出表中a,b,c的值;
(2)补全条形图;
(3)商场经理准备购进同一品牌的旅游鞋1500双,请根据市场实际情况估计他应该购进38码的鞋多少双?