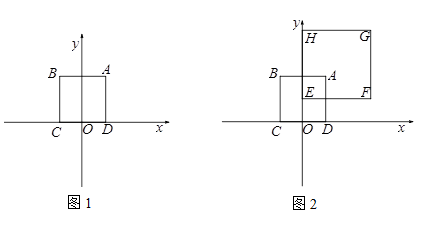如图，在平面直角坐标系中，一次函数 和 的图象相交于点 ，反比例函数 的图象经过点 ．
（1）求反比例函数的表达式；
（2）设一次函数 的图象与反比例函数 的图象的另一个交点为 ，连接 ，求 的面积．
端午节期间，某校“慈善小组”筹集善款600元，全部用于购买粽子到福利院送给老人.购买大枣粽子和豆沙粽子各花300元，已知大枣粽子比豆沙粽子每盒贵5元，结果购买的大枣粽子比豆沙粽子少2盒．请求出两种口味的粽子每盒各多少元?
已知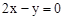
，求代数式
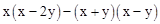的值.
求不等式组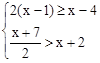
的整数解．
如图，点A、C、D、B四点共线，且AC=DB，∠A=∠B，∠E=∠F．求证：DE=CF．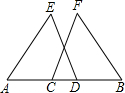
对于半径为r的⊙P及一个正方形给出如下定义：若⊙P上存在到此正方形四条边距离都相等的点，则称⊙P是该正方形的“等距圆”．如图1，在平面直角坐标系xOy中，正方形ABCD的顶点A的坐标为（2，4），顶点C、D在x轴上，且点C在点D的左侧.
（1）当r=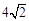
时，
①在P1（0，-3），P2（4，6），P3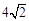（，2）中可以成为正方形ABCD的“等距圆”的圆心的是_______________；
②若点P在直线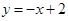
上，且⊙P是正方形ABCD的“等距圆”，则点P的坐标为_______________；
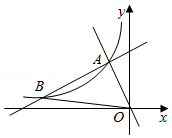
（2）如图2，在正方形ABCD所在平面直角坐标系xOy中，正方形EFGH的顶点F的坐标为（6，2），顶点E、H在y轴上，且点H在点E的上方.
①若⊙P同时为上述两个正方形的“等距圆”，且与BC所在直线相切，求⊙P 在y轴上截得的弦长；
②将正方形ABCD绕着点D旋转一周，在旋转的过程中，线段HF上没有一个点能成为它的“等距圆”的圆心，则r的取值范围是_______________．