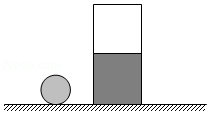
如图甲所示,是测量高于警戒水位的装置原理图。在横截面积为 的长方体绝缘容器的内部边缘左右两正对面,竖直插有两块薄金属板(电阻不计)并与外部电路连接,容器底部有一个小孔与湖水相通,容器的底部与警戒水位相平。电源电压 ,小灯泡 标有“ ”的字样(假设小灯泡的电阻不变),湖水的密度为 .两金属板间的湖水电阻 与容器内水柱的高度 的倒数的变化关系如图乙所示。则:

(1)湖水水位比警戒水位高出多少时,小灯泡正常发光?
(2)当进入容器内的水达到 时,容器内的湖水消耗的电功率是多大?
2016年6月28日,备受关注的南宁地铁1号线东段将进入试运行阶段。若南湖站到金湖广场站的路程为380m,地铁1号专用列车从南湖站到金湖广场站的运行时间约为40s,列车牵引力约为2×104N.求这段路程中:
(1)列车行驶的平均速度;
(2)列车牵引力所做的功。
正方体塑料块A边长lA=0.1m,它所受的重力GA=6N.另一圆柱体B高hB=0.1m,底面积SB=5×10﹣3m2,它的密度ρB=1.6×103kg/m3.已知水的密度ρ水=1.0×103kg/m3,取g=10N/kg。
(1)圆柱体B所受的重力是多少?
(2)将塑料块A浸没在水中,通过计算说明释放后它上浮还是下沉?
(3)如图所示,将圆柱体B置于塑料块A正上方,放入一个水平放置的水槽中,向水槽缓慢注水,请写出塑料块A对水槽底部的压强p。

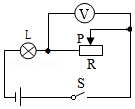
如图所示,灯泡L标有“8V,4W”字样,电源电压U=9V,电源电压及灯泡电阻均保持不变,滑动变阻器最大阻值为10Ω,电压表量程是0~3V,求:
(1)灯泡的额定电流;
(2)为使灯泡正常发光,滑动变阻器连入电路的阻值;
(3)为使整个电路安全,滑动变阻器的阻值变化范围。
2016年五一假期,三千多名自行车爱好者在风景秀美的环江滨水大道等路段参加“快乐骑行,拥抱柳江”的健身运动。小龙同学骑公共自行车参加了6km骑行体验运动。他在某路段匀速直线行驶。在50s内通过了300m的路程,所受阻力大小为40N。
(1)小龙同学在50s内骑车行驶的速度是多少?若他按此速度完成6km骑行体验运动,需要多长时间?
(2)小龙同学在50s内骑车行驶的功率是多少?
如图所示,重为4N、高为0.24m、底面积为0.02m2的圆柱形容器放在水平桌面上,容器内装有4kg的水(不计容器壁的厚度,g取10N/kg,水的密度为1.0×103kg/m3),求:
(1)水对容器底部产生的压强p水;
(2)现将一密度为2.0×103kg/m3的实心小球轻轻地放入容器中,静止后有0.2kg的水溢出,此时圆柱形容器对桌面的压强。