如图所示，一倾角为 的固定斜面的底端安装一弹性挡板， 、 两物块的质量分别为 和 ， 静止于斜面上 处。某时刻， 以沿斜面向上的速度 与 发生弹性碰撞。 与斜面间的动摩擦因数等于 ，设最大静摩擦力等于滑动摩擦力。 与斜面间无摩擦，与挡板之间的碰撞无动能损失。两物块均可以看作质点，斜面足够长， 的速度减为零之前 不会与之发生碰撞。重力加速度大小为 。
（1）求 与 第一次碰撞后瞬间各自的速度大小 、 ；
（2）求第 次碰撞使物块 上升的高度 ；
（3）求物块 从 点上升的总高度 ；
（4）为保证在 的速度减为零之前 不会与之发生碰撞，求 点与挡板之间的最小距离 。
一个物体从塔顶上下落，在到达地面前最后1 s内通过的位移是整个位移的
，求：塔高为多少米？（g=10m/s2）
一辆汽车在平直公路上做匀变速直线运动，公路边每隔15m有一棵树，如图所示，汽车通过AB两相邻的树用了3s，通过BC两相邻的树用了2s，求汽车运动的加速度和通过树B时的速度为多少?
一劲度系数k＝800 N/m的轻质弹簧两端分别连接着质量均为12 kg的物体A、B，将它们竖直静止放在水平面上，如图所示．现将一竖直向上的变力F作用在A上，使A开始向上做匀加速运动，经0.40 s物体B刚要离开地面．g＝10 m/s2，
试求：
（1）物体B刚要离开地面时，A物体的速度vA；
（2）物体A重力势能的改变量；
如图所示，一个质量m=1kg的长木板静止在光滑的水平面上，并与半径为R=1.8m的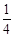
光滑圆弧形固定轨道接触（但不粘连），木板的右端到竖直墙的距离为s=0.08m；另一质量也为m的小滑块从轨道的最高点由静止开始下滑，从圆弧的最低点A滑上木板。设长木板每次与竖直墙的碰撞时间极短且无机械能损失。木板的长度可保证物块在运动的过程中不与墙接触。已知滑块与长木板间的动摩擦因数
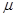=0.1，g取10m/s2。试求：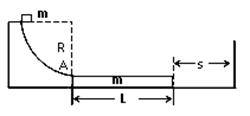
（1）滑块到达A点时对轨道的压力大小；
（2）当滑块与木板达到共同速度（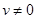
）时，滑块距离木板左端的长度是多少？
如图所示，质量为m的小物块在粗糙水平桌面上做直线运动，经距离l后以速度v飞离桌面，最终落在水平地面上。已知l=1.4m，v=3.0m/s，m=0.10kg，物块与桌面间的动摩擦因数
=0.25，桌面高h=0.45m，不计空气阻力，重力加速度g取10m/s2．求：
（1）小物块落地点距飞出点的水平距离s；
（2）小物块的初速度大小v0．