问题解决:如图1,在矩形 中,点 , 分别在 , 边上, , 于点 .

(1)求证:四边形 是正方形;
(2)延长 到点 ,使得 ,判断 的形状,并说明理由.
类比迁移:如图2,在菱形 中,点 , 分别在 , 边上, 与 相交于点 , , , , ,求 的长.
化简 .
.
如图(1)四边形ABCD中,已知∠ABC+∠ADC=180°,AB=AD,DA⊥AB,点E在CD的延长线上,∠BAC=∠DAE.
(1)求证:△ABC≌△ADE;
(2)求证:CA平分∠BCD;
(3)如图(2),设AF是△ABC的BC边上的高,求证:EC=2AF.
已知x=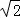 ﹣1,求下列问题:
﹣1,求下列问题:
(1)证明:x2+2x=1;
(2)利用(1)的结论,化简x4+2x3+2x﹣1;
(3)试判断x= ﹣1是不是方程
﹣1是不是方程 ﹣1=
﹣1= 的解?
的解?
如图,A、F、E、B四点共线,AC⊥CE,BD⊥DF,AE=BF,AC=BD.
(1)求证:△ACE≌△BDF;
(2)求证:△ACF≌△BDE.
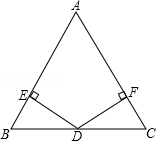
△ABC中,AB=AC,D是BC中点,DE⊥AB于E,DF⊥AC于F,求证:DE=DF.