猕猴嬉戏是王屋山景区的一大特色,猕猴玩偶非常畅销.小李在某网店选中 , 两款猕猴玩偶,决定从该网店进货并销售.两款玩偶的进货价和销售价如下表:
类别 价格 |
款玩偶 |
款玩偶 |
进货价(元 个) |
40 |
30 |
销售价(元 个) |
56 |
45 |
(1)第一次小李用1100元购进了 , 两款玩偶共30个,求两款玩偶各购进多少个.
(2)第二次小李进货时,网店规定 款玩偶进货数量不得超过 款玩偶进货数量的一半.小李计划购进两款玩偶共30个,应如何设计进货方案才能获得最大利润,最大利润是多少?
(3)小李第二次进货时采取了(2)中设计的方案,并且两次购进的玩偶全部售出,请从利润率的角度分析,对于小李来说哪一次更合算?
(注:利润率
近年来,某县为发展教育事业,加大了对教育经费的投入,2010年投入6000万元,2012年投入8640万元.
(1)求2010年至2012年该县投入教育经费的年平均增长率;
(2)该县预计2013年投入教育经费不低于9500万元,若继续保持前两年的平均增长率,该目标能否实现?请通过计算说明理由.
某中学举行数学知识竞赛,所有参赛学生分别设有一、二、三等奖和纪念奖,获奖情况已汇制成如图所示的两幅不完整的统计图,根据图中所给信息解答下列问题: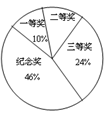
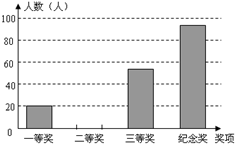
(1)这次数学知识竞赛获得二等奖人数是多少?
(2)请将条形统计图补充完整;
(3)若给所有参赛学生每人发一张卡片,各自写自己名字,然后把卡片放入一个不透明的袋子内,摇匀后任意摸取一张卡片,求摸出的卡片上是写有一等奖学生名字的概率。
如图,在平面直角坐标系中,一次函数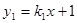 的图象与
的图象与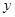 轴交于点A,与
轴交于点A,与 轴交于点B,与反比例函数
轴交于点B,与反比例函数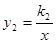 的图象分别交于点M、N,已知△AOB的面积为1,点M的纵坐标为2.
的图象分别交于点M、N,已知△AOB的面积为1,点M的纵坐标为2.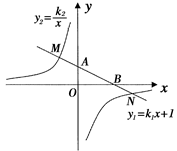
(1)求一次函数与反比例函数的解析式;
(2)直接写出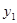 >
>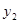 时,
时, 的取值范围.
的取值范围.
已知:x=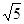 +
+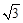 ,y=
,y=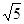 -
-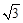 ,求:
,求: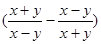 ·
·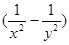 的值.
的值.
小明在路灯AB下玩耍时发现自己的影长DF的长是3米,沿着BD方向来到点F处再测得自己的影长FG是4米.如果小明的身高是1.8米,求路灯AB的高度.