如图,抛物线 与直线 相交于点 和点 .
(1)求 和 的值;
(2)求点 的坐标,并结合图象写出不等式 的解集;
(3)点 是直线 上的一个动点,将点 向左平移3个单位长度得到点 ,若线段 与抛物线只有一个公共点,直接写出点 的横坐标 的取值范围.

如图,在单位长度为1的正方形网格中,一段圆弧经过格点A、B、C.
(1)画出该圆弧所在圆的圆心D的位置(不用写作法,保留作图痕迹),并连接AD、CD.
(2)请在(1)的基础上,完成下列问题:
①以点O为原点、水平方向所在直线为x轴、竖直方向所在直线为y轴,建立平面直角坐标系,写出点的坐标:C、D;
②⊙D的半径为(结果保留根号);
③若用扇形ADC围成一个圆锥的侧面,则该圆锥的底面圆半径是;
④若E(7,0),试判断直线EC与⊙D的位置关系并说明你的理由.
某商店准备进一批季节性小家电,单价40元.经市场预测,销售定价为52元时,可售出180个,定价每增加1元,销售量净减少10个;定价每减少1元,销售量净增加10个.因受库存的影响,每批次进货个数不得超过180个,商店若将准备获利2000元,则应进货多少个?定价为多少元?
如图,在□ABCD中,过点B作BE⊥CD于E,F为AE上一点,且∠BFE=∠C.
(1)求证:△ABF∽△EAD;
(2)若AB=4,∠BAE=30º,求AE的长;
(3)在(1)(2)的条件下,若AD=3,求BF的长.
如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,且∠D=2∠A.
(1)求∠D的度数;
(2)若CD=2,求BD的长.
已知关于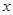 的一元二次方程
的一元二次方程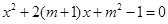 .
.
(1)若方程有实数根,求实数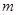 的取值范围;
的取值范围;
(2)若方程两实数根分别为 、
、 ,且满足
,且满足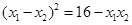 ,求实数
,求实数 的值.
的值.