如图,抛物线 与 轴交于原点 和点 ,且其顶点 关于 轴的对称点坐标为 .
(1)求抛物线的函数表达式;
(2)抛物线的对称轴上存在定点 ,使得抛物线 上的任意一点 到定点 的距离与点 到直线 的距离总相等.
①证明上述结论并求出点 的坐标;
②过点 的直线 与抛物线 交于 , 两点.
证明:当直线 绕点 旋转时, 是定值,并求出该定值;
(3)点 是该抛物线上的一点,在 轴, 轴上分别找点 , ,使四边形 周长最小,直接写出 , 的坐标.

某中学开展“中国梦、我的梦”演讲比赛,甲、乙两班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如下图所示.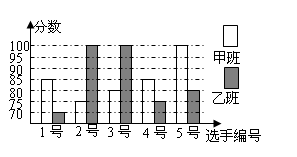
(1)根据下图,分别求出两班复赛的平均成绩和方差;
(2)根据(1)的计算结果,分析哪个班级的复赛成绩较好?
已知关于x的方程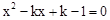 .
.
(1)求证:无论k取什么实数值,这个方程总有实数根;
(2)当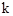 =3时,△ABC的每条边长恰好都是方程
=3时,△ABC的每条边长恰好都是方程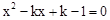 的根,求△ABC的周长.
的根,求△ABC的周长.
当a=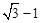 时,求
时,求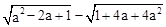 的值.
的值.
解方程:
(1)2x2=5x(2)m2+3m-1=0(3)9(x+1)2-(x-2)2=0
如图,已知直线l分别与x轴、y轴交于A、B两点,与双曲线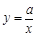 (a≠0,x>0)分别交于D、E两点.
(a≠0,x>0)分别交于D、E两点.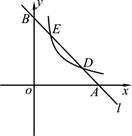
(1)若点D的坐标为(4,1),点E的坐标为(1,4):
① 分别求出直线l与双曲线的解析式;
② 若将直线l向下平移m(m>0)个单位,当m为何值时,直线l与双曲线有且只有一个交点?
(2)假设点A的坐标为(a,0),点B的坐标为(0,b),点D为线段AB的n等分点,请直接写出b的值.