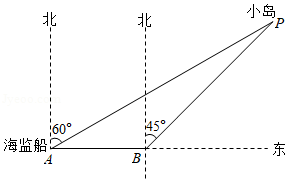
某海域有一小岛 ，在以 为圆心，半径 为 海里的圆形海域内有暗礁．一海监船自西向东航行，它在 处测得小岛 位于北偏东 的方向上，当海监船行驶 海里后到达 处，此时观测小岛 位于 处北偏东 方向上．
（1）求 ， 之间的距离 ；
（2）若海监船由 处继续向东航行是否有触礁危险？请说明理由．如果有触礁危险，那么海监船由 处开始沿南偏东至多多少度的方向航行能安全通过这一海域？
已知AB∥DE，BC∥EF，D，C在AF上，且AD=CF，求证：△ABC≌△DEF．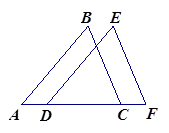
如图1，A、B两点同时从原点0出发，点A以每秒x个单位长度沿x轴的负方向运动，点B以每秒y个单位长度沿y轴的正方向运动．
（1）若
，试分别求1秒后A、B两点的坐标．
（2）如图2，AP、BP分别是∠BAC和∠DBA的平分线，试问：点A、B在运动过程中，∠P的大小是否会发生变化?若不变化，请求出其值；若发生变化，请说明理由．
（3）如图3，延长BA至点E，在∠ABO的内部做射线BF交x轴于点C．若∠EAC、∠FCA和∠ABC的平分线相交于点G，过点G作GH⊥BE于点H，试问∠AGH与∠BGC有何数量关系?请写出你的结论并说明理由．
（1）如图，已知∠AOB，请你利用图①，用尺规作出∠AOB的平分线0P，并画一对以OP所在直线为对称轴的全等三角形；
（2）参考（1）中画全等三角形的方法，解答下列问题：如图②，在ABC中，∠ACB是直角，∠B =60°，AD、CE分别是∠BAC与∠BCA的平分 线，AD和CE相交于点F，请猜想FE与FD有怎样的数量关系，并加以说明．
如图，∠ACB =90°，AC=BC，BE⊥CE，AD⊥CE于D，AD=2.5cm，DE=1.7cm，求BE的长.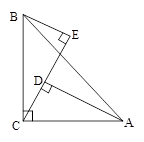
如图，D是AB上一点，DF交AC于点E，DE=FE,FC∥AB。AE与CE有什么关系？证明你的结论。