如图, 是以 为直径的 上一点,过点 的切线 交 的延长线于点 ,过点 作 交 的延长线于点 ,垂足为点 .
(1)求证: ;
(2)若 的直径 为9, .
①求线段 的长;
②求线段 的长.

如图,在▱ABCD中,过A、C、D三点的⊙O交AB于点E,连接DE、CE,∠CDE=∠BCE.
(1)求证:AD=CE;
(2)判断直线BC与⊙O的位置关系,并说明理由;
(3)若BC=3,DE=6,求BE的长.
在平面直角坐标系xOy中,对于任意三点A、B、C的“矩面积”,给出如下定义:“水平底”a:任意两点横坐标差的最大值,“铅垂高”h:任意两点纵坐标差的最大值,则“矩面积”S=ah.
例如:三点坐标分别为A(1,2),B(﹣3,1),C(2,﹣2),则“水平底”a=5,“铅垂高”h=4,“矩面积”S=ah=20.
(1)已知点A(1,2),B(﹣3,1),P(0,t).
①若A、B、P三点的“矩面积”为12,求点P的坐标;
②A、B、P三点的“矩面积”的最小值为.
(2)已知点E(4,0),F(0,2)M(m,4m),其中m>0.若E、F、M三点的“矩面积”的为8,求m的取值范围.
某新建火车站站前广场需要绿化的面积为46000米2,施工队在绿化了22000米2后,将每天的工作量增加为原来的1.5倍,结果提前4天完成了该项绿化工程.
(1)该项绿化工程原计划每天完成多少米2?
(2)该项绿化工程中有一块长为20米,宽为8米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为56米2,两块绿地之间及周边留有宽度相等的人行通道(如图所示),问人行通道的宽度是多少米?
如图,将▱ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
(1)求证:△ABF≌△ECF;
(2)若∠AFC=2∠D,连接AC、BE,求证:四边形ABEC是矩形.
(1)甲、乙、丙三只不透明的口袋中都装有1个白球、1个红球,它们除颜色外都相同,搅匀后分别从三只口袋中任意摸出1个球,求从三只口袋摸出的都是红球的概率.
(2)甲、乙、丙、丁四位同学分别站在正方形场地的四个顶点A、B、C、D处,每个人都以相同的速度沿着正方形的边同时出发随机走向相邻的顶点处,那么甲、乙、丙、丁四位同学互不相遇的概率是.
①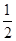 ;②
;② ;③
;③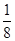 ;④
;④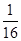 .
.