在平面直角坐标系中,抛物线 与 轴交于点 和点 ,与 轴交于点 ,顶点 的坐标为 .
(1)直接写出抛物线的解析式;
(2)如图1,若点 在抛物线上且满足 ,求点 的坐标;
(3)如图2, 是直线 上一个动点,过点 作 轴交抛物线于点 , 是直线 上一个动点,当 为等腰直角三角形时,直接写出此时点 及其对应点 的坐标.

计算(每题3分,共15分)
(1)-7+3+(-6)-(-7)(2)8+
 ;
;
(3)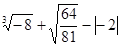 (4)
(4) (用简便方法计算)
(用简便方法计算)
(5)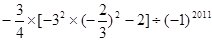
在数轴上表示下列各数,并把这些数按从小到大顺序进行排列,用“<”连接。
π, 4, -(-2), 0, 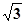 ,
,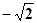
如图1,△ABC的边BC在直线 上,AC ⊥BC,且AC=BC;△EFP的边FP也在直线
上,AC ⊥BC,且AC=BC;△EFP的边FP也在直线 上,边EF与边AC重合,且EF=FP.
上,边EF与边AC重合,且EF=FP.
(1)将△EFP沿直线 向左平移到图2的位置时,EP交AC于点Q,连结AP,BQ.猜想 BQ 与AP所满足的数量关系和位置关系。(直接写出结论)
向左平移到图2的位置时,EP交AC于点Q,连结AP,BQ.猜想 BQ 与AP所满足的数量关系和位置关系。(直接写出结论)
APBQ,APBQ;
(2)将△EFP沿直线 向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连结AP,BQ.你认为(1)中所猜想的BQ与AP的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.
向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连结AP,BQ.你认为(1)中所猜想的BQ与AP的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.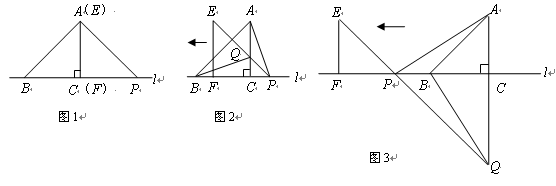
在一次数学活动中,黑板上画着如图所示的图形,活动前刘老师在准备的四张纸片上分别写有如下四个等式中的一个等式:
①AB=DC;②∠ABE=∠DCE;③AE=DE;④∠A=∠D
小明同学闭上眼睛从四张纸片中随机抽取一张,再从剩下的纸片中随机抽取另一张.请结合图形解答下列两个问题: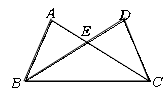
(1)请你写出在抽取的两张纸片上的等式为条件不能判断△BCE是等腰三角形的所有情形:;(用序号表示)
(2)当抽得①和②时,用①,②作为条件能判定△BCE是
等腰三角形吗?说说你理的由;
张明、王成两位同学八年级10次数学单元自我检测的成绩(成绩均为整数,且个位数为0)分别如下图所示: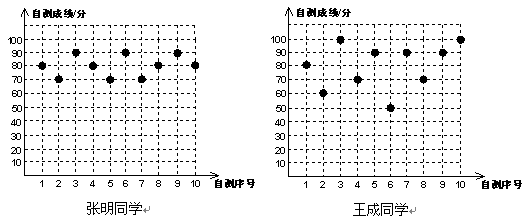
(1)根据上图中提供的数据填写下表:
| 平均成绩 |
中位数 |
众数 |
方差(S2) |
|
| 张明 |
80 |
|||
| 王成 |
85 |
260 |
(2)如果将90分以上(含90分)的成绩视为优秀,则优秀率高的同学是________.
(3)根据图表信息,请你对这两位同学各提一条不超过20个字的学习建议.