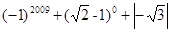为庆祝中国共产党建党100周年,某校举行了“红色华诞,党旗飘扬”党史知识竞赛.为了解竞赛成绩,抽样调查了七、八年级部分学生的分数,过程如下:
(1)收集数据.
从该校七、八年级学生中各随机抽取20名学生的分数,其中八年级的分数如下:
81 83 84 85 86 87 87 88 89 90
92 92 93 95 95 95 99 99 100 100
(2)整理、描述数据.
按下表分段整理描述样本数据:
分数 人数 年级 |
|
|
|
|
七年级 |
4 |
6 |
2 |
8 |
八年级 |
3 |
|
4 |
7 |
(3)分析数据.
两组样本数据的平均数中位数、众数、方差如表所示:
年级 |
平均数 |
中位数 |
众数 |
方差 |
七年级 |
91 |
89 |
97 |
40.9 |
八年级 |
91 |
|
|
33.2 |
根据以上提供的信息,解答下列问题:
①填空: , , ;
②样本数据中,七年级甲同学和八年级乙同学的分数都为90分, 同学的分数在本年级抽取的分数中从高到低排序更靠前(填“甲”或“乙” ;
③从样本数据分析来看,分数较整齐的是 年级(填“七”或“八” ;
④如果七年级共有400人参赛,则该年级约有 人的分数不低于95分.
(本题8分)某商场销售某种品牌的纯牛奶,已知进价为每箱40元,市场调查发现,若每箱以50元销售,平均每天可销售90箱,价格每降低1元,平均每天多售3箱,价格每升高1元,平均每天少售3箱。
①写出平均每天的销售量y与每箱售价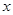 之间关系;
之间关系;
②求出商场平均每天销售这种牛奶的利润w与每箱售价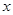 之间的关系;
之间的关系;
③求在的情况下当牛奶每箱售价定为多少时可达到最大利润,最大利润是多少元?
(本题8分)如图,AB为⊙O的直径,CD⊥AB于点E,交⊙O于点D,OF⊥AC于点F.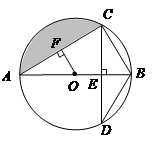
(1)请写出两条与BC有关的正确结论;
(2)当∠D=30°,BC=1时,求圆中阴影部分的面积.
(本题6分)如图,一次函数y=ax+b的图像与反比例函数 的图像交于M、N两点。
的图像交于M、N两点。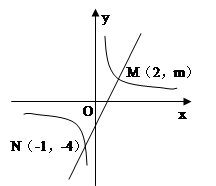
求:(1)反比例函数与一次函数的解析式。
(2)根据图像写出反比例函数的值不小于一次函数的值的x的取值范围。
(本题6分)在某一电路中,保持电压不变,电流I(安培)与电阻R(欧姆)成反比例.当电阻R=6欧姆时,电流 I=2安培.
(l)求I与R之间的函数关系式;
(2)当电流I="1.5" 安培时,求电阻R的值;
(3)如果电路中用电器限制电流不得超过10安培,那么用电器的可变电阻应控制在什么范围内?
(本题6分)计算: