如图,在 中, , .
(1)通过观察尺规作图的痕迹,可以发现直线 是线段 的 ,射线 是 的 ;
(2)在(1)所作的图中,求 的度数.

已知:如图,抛物线y=ax2+bx+2与x轴的交点是A(3,0)、B(6,0),与y轴的交点是C.
(1)求抛物线的函数关系式;
(2)设P(x,y)(0<x<6)是抛物线上的动点,过点P作PQ∥y轴交直线BC于点Q.
①当x取何值时,线段PQ长度取得最大值?其最大值是多少?
②是否存在点P,使△OAQ为直角三角形?若存在,求点P坐标;若不存在,说明理由.
已知:在矩形ABCD中,AB=10,BC=12,四边形EFGH的三个顶点E、F、H分别在矩形ABCD边AB、BC、DA上,AE=2.
(1)如图①,当四边形EFGH为正方形时,求△GFC的面积;
(2)如图②,当四边形EFGH为菱形,且BF=a时,求△GFC的面积(用a表示);
(3)在(2)的条件下,△GFC的面积能否等于2?请说明理由.
如图,已知一次函数y=kx+b的图象交反比例函数y=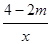 (x>0)的图象于点A、B,交x轴于点C.
(x>0)的图象于点A、B,交x轴于点C.
(1)求m的取值范围;
(2)若点A的坐标是(2,-4),且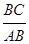 =
= ,求m的值和一次函数的解析式.
,求m的值和一次函数的解析式.
某商店需要购进甲、乙两种商品共160件,其进价和售价如下表:
| 甲 |
乙 |
|
| 进价(元/件) |
15 |
35 |
| 售价(元/件) |
20 |
45 |
(1)若商店计划销售完这批商品后能获利1100元,问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于4300元,且销售完这批商品后获利多于1260元,请问有哪几种购货方案? 并直接写出其中获利最大的购货方案.
一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=30°,∠A=45°,AC=12 .
.
求:(1)BC的长;(2)CD的长.