某超市从厂家购进 、 两种型号的水杯,两次购进水杯的情况如表:
进货批次 |
型水杯(个 |
型水杯(个 |
总费用(元 |
一 |
100 |
200 |
8000 |
二 |
200 |
300 |
13000 |
(1)求 、 两种型号的水杯进价各是多少元?
(2)在销售过程中, 型水杯因为物美价廉而更受消费者喜欢.为了增大 型水杯的销售量,超市决定对 型水杯进行降价销售,当销售价为44元时,每天可以售出20个,每降价1元,每天将多售出5个,请问超市应将 型水杯降价多少元时,每天售出 型水杯的利润达到最大?最大利润是多少?
(3)第三次进货用10000元钱购进这两种水杯,如果每销售出一个 型水杯可获利10元,售出一个 型水杯可获利9元,超市决定每售出一个 型水杯就为当地"新冠疫情防控"捐 元用于购买防控物资.若 、 两种型号的水杯在全部售出的情况下,捐款后所得的利润始终不变,此时 为多少?利润为多少?
解下列分式方程:(1) ;(2)
;(2) .
.
化简:(1) ;(2)
;(2)
 .
.
解下列不等式(组),并把它的解集在数轴上表示出来。
(1) (2)
(2)
如图,已知函数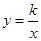 与
与 相交于A,B两点,且A(3,4)过A作AC⊥x轴于C点,
相交于A,B两点,且A(3,4)过A作AC⊥x轴于C点,
(1)求反比例函数的关系式.
(2)观察图象,当x在什么范围内时正比例函数值大于反比例函数的值.
(3)在坐标轴上是否存在一点E使得以B,O,E为顶点的三角形与△AOC相似(三角形全等除外)? 若存在,求出E点坐标;若不存在,请说明理由.
如图,在△ABC和△DCB中,下面有三个条件,请你以其中两个为题设,第三个作为结论,写出一个正确的命题,并加以证明.
①AB=DC;②AC = DB;③∠ABC=∠DCB.
已知:
求证:
证明: