古埃及人的"纸草书"中记载了一个数学问题:一个数,它的三分之二,它的一半,它的七分之一,它的全部,加起来总共是33.若设这个数是 ,则所列方程为
| A. |
|
B. |
|
| C. |
|
D. |
|
在△ABC中,若|sinB﹣ |与(
|与( ﹣cosA)2互为相反数,则∠C等于()
﹣cosA)2互为相反数,则∠C等于()
A.120° B.90° C.60° D.45°
cotβ= ,则锐角β等于()
,则锐角β等于()
| A.0° | B.30° | C.45° | D.60° |
如图,设点A(m,n)是锐角α的一条边上任意一点,则 的值()
的值()
| A.只与角α的大小有关 |
| B.只与点A在角α的边上的位置有关 |
| C.与角α的大小及点A在角α的边上的位置有关 |
| D.与角α的大小及点A在角α的边上的位置无关 |
如图,AB是⊙O的直径,CD是弦,AD和BC相交于点E,已知AB=5,CD=2,则cos∠BED=()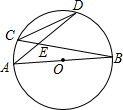
A. |
B. |
C. |
D.无法计算 |
在Rt△ABC中,若将三边的长度都缩小到原来的 倍,则锐角A的正弦值、余弦值及正切值的情况()
倍,则锐角A的正弦值、余弦值及正切值的情况()
| A.都扩大2倍 | B.都缩小 倍 倍 |
C.都不变 | D.不确定 |