如图，已知正方形ABCD，点E是BC边上一点，将ΔABE沿直-优题课

题文

如图，已知正方形 $ABCD$ ，点 $E$ 是 $BC$ 边上一点，将 $ΔABE$ 沿直线 $AE$ 折叠，点 $B$ 落在 $F$ 处，连接 $BF$ 并延长，与 $∠ DAF$ 的平分线相交于点 $H$ ，与 $AE$ ， $CD$ 分别相交于点 $G$ ， $M$ ，连接 $HC$ ．

（1）求证： $AG = GH$ ；

（2）若 $AB = 3$ ， $BE = 1$ ，求点 $D$ 到直线 $BH$ 的距离；

（3）当点 $E$ 在 $BC$ 边上（端点除外）运动时， $∠ BHC$ 的大小是否变化？为什么？

科目数学题型解答题难度困难

知识点：相似三角形的判定与性质正方形的性质相似形综合题

登录免费查看答案和解析

相关试题

（本题7分）化简求值.
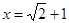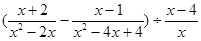已知：，求式子的值.

本题6分）如图，平面直角坐标系中，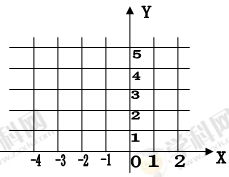

（1）取点A（2，1）、点B（－3，4），则线段AB的长为；
（2）若点A的坐标为A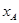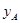（，），点B的坐标为A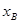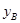（，），则线段AB的长为（用含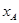、、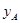、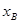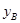的式子表示）；
（3）△ABC中，已知点A（2，－2）、点B（－3，－1）、点C（－1、－4），请运用（2）中的结论，不画图，用代数方法判断并证明△ABC的形状.

（本题7分）如图，长方形纸片ABCD中，AD＝8，折叠纸片使AB边与对角线AC重合，点B落在点F处，折痕为AE，EF＝3，求AB的长.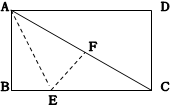

（本题6分）在实数范围内分解因式：（1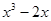）；（2）.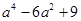

（本题12分）已知抛物线y=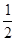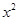＋c与x轴交于A（－1，0），B两点，交y轴于点C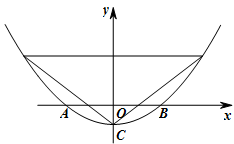

（1）求抛物线的解析式
（2）点E（m，n）是第二象限内一点，过点E作EF⊥x轴交抛物线于点F，过点F作FG⊥y轴于点G，连接CE、CF，若∠CEF=∠CFG，求n的值并直接写出m的取值范围（利用图1完成你的探究）
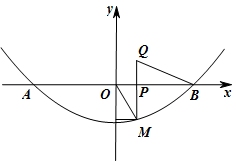
（3）如图2，点P是线段OB上一动点（不包括点O、B），PM⊥x轴交抛物线于点M，∠OBQ＝∠OMP，BQ交直线PM于点Q，设点P的横坐标为t，求△PBQ的周长

试卷网试题网古诗词网作文网范文网