如图, 是 直径,弦 ,垂足为点 .弦 交 于点 ,点 在 延长线上,且 .
(1)求证: 为 切线;
(2)若 , , ,求 的长.

已知:如图,在四边形ABCD中,∠ABC=90°,CD⊥AD,AD2+CD2=2AB2.
(1)求证:AB=BC;
(2)当BE⊥AD于E时,试证明:BE=AE+CD.
如图,AB是⊙O的直径,弦CD⊥AB于点E,过点B作⊙O的切线,交AC的延长线于点F.已知OA=3,AE=2,
(1)求CD的长;
(2)求BF的长.
某商店在开业前,所进衣服、裤子与鞋子的数量共480份,各种货物进货比例
如图
销售人员(衣服6人,裤子4人,鞋子2人)用了5天的时间销售,销售货物的情况如图(2)与
表格.
(1)所进衣服的件数是多少?
(2)把图(2)补充完整;
(3)把表格补充完整;
(4)若销售人员不变,同样的销售速度销售,请通过计算说明哪种货物最先售完?
为倡导“低碳生活”,常选择以自行车作为代步工具,如图1所示是一辆自行车的实物图.车架档AC与CD的长分别为45cm,60cm,且它们互相垂直,座杆CE的长为20cm,点A,C,E在同一条直线上,且∠CAB=75°,如图2.
(1)求车架档AD的长;
(2)求车座点E到车架档AB的距离.
(结果精确到1 cm.参考数据: sin75°="0.966," cos75°=0.259,tan75°=3.732)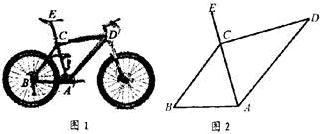
解不等式组,并把解集在数轴上表示出来.