如图, 为 的直径, 为 上一点,连接 , , 为 延长线上一点,连接 ,且 .
(1)求证: 是 的切线;
(2)若 的半径为 , 的面积为 ,求 的长;
(3)在(2)的条件下, 为 上一点,连接 交线段 于点 ,若 ,求 的长.

(本小题满分8分,每题4分)
(1)化简: ;
;
(2)关于 的一元二次方程
的一元二次方程  有两个不相等的实数根,求
有两个不相等的实数根,求 的取值范围
的取值范围
已知:线段 ,直线
,直线 外一点A.
外一点A.
求作:Rt△ABC,使直角边为AC(AC⊥ ,垂足为C)斜边AB=c.
,垂足为C)斜边AB=c.
如图,在平面直角坐标系中,已知抛物线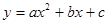 交
交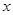 轴于
轴于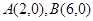 两点,交
两点,交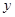 轴于点
轴于点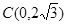 .
.
(1)求此抛物线的解析式;
(2)若此抛物线的对称轴与直线 交于点D,作⊙D与x轴相切,⊙D交
交于点D,作⊙D与x轴相切,⊙D交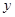 轴于点E、F两点,求劣弧
轴于点E、F两点,求劣弧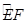 的长;
的长;
(3)P为此抛物线在第二象限图像上的一点,PG垂直于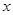 轴,垂足为点G,试确定P点的位置,使得△PGA的面积被直线AC分为1︰2两部分.
轴,垂足为点G,试确定P点的位置,使得△PGA的面积被直线AC分为1︰2两部分.
在 ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连结EG、GF、FH、HE.
ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连结EG、GF、FH、HE.
(1)如图①,试判断四边形EGFH的形状,并说明理由;
(2)如图②,当EF⊥GH时,四边形EGFH的形状是;
(3)如图③,在(2)的条件下,若AC=BD,四边形EGFH的形状是;
(4)如图④,在(3)的条件下,若AC⊥BD,试判断四边形EGFH的形状,并说明理由.
为打造“书香校园”,某学校计划用不超过1900本科技类书籍和1620本人文类书籍,组建中、小型两类图书角共30个.已知组建一个中型图书角需科技类书籍80本,人文类书籍50本;组建一个小型图书角需科技类书籍30本,人文类书籍60本.
(1)问符合题意的组建方案有几种?请你帮学校设计出来;
(2)若组建一个中型图书角的费用是860元,组建一个小型图书角的费用是570元,试说明在(1)中哪种方案费用最低?最低费用是多少元?