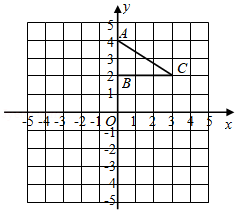
如图,在平面直角坐标系中, 的顶点坐标分别是 , , .
(1)将 以 为旋转中心旋转 ,画出旋转后对应的△ ;
(2)将 平移后得到△ ,若点 的对应点 的坐标为 ,求△ 的面积.
某天,北海舰队在中国南海例行训练,位于 处的济南舰突然发现北偏西 方向上的 处有一可疑舰艇,济南舰马上通知位于正东方向200海里 处的西安舰,西安舰测得 处位于其北偏西 方向上,请问此时两舰距 处的距离分别是多少?

如图,在菱形 中,点 、 分别在 、 上,且 ,求证: .

先化简,再求值: ,其中 , 满足 .
计算: .
已知点 是线段 的中点,点 是直线 上的任意一点,分别过点 和点 作直线 的垂线,垂足分别为点 和点 .我们定义垂足与中点之间的距离为"足中距".
(1) 猜想验证 如图1,当点 与点 重合时,请你猜想、验证后直接写出"足中距" 和 的数量关系是 .
(2) 探究证明 如图2,当点 是线段 上的任意一点时,"足中距" 和 的数量关系是否依然成立,若成立,请给出证明;若不成立,请说明理由.
(3) 拓展延伸 如图3,①当点 是线段 延长线上的任意一点时,"足中距" 和 的数量关系是否依然成立,若成立,请给出证明;若不成立,请说明理由;
②若 ,请直接写出线段 、 、 之间的数量关系.
