我国古代数学家赵爽用弦图给出了勾股定理的证明.弦图是由四个全等的直角三角形和中间的一个小正方形拼成的一个大正方形(如图所示).若直角三角形直角边的长分别是3,4,记大正方形的面积为 ,小正方形的面积为 ,则 ___________.

给出以下四个命题:
①为了解600名学生对学校某项教改试验的意见,打算从中抽取一个容量为30的样本,考虑用系统抽样,则分段的间隔k为30;
②二项式 的展开式中含
的展开式中含 项的系数是
项的系数是 ;
;
③在某项测量中,测量结果 服从正态分布N(2,
服从正态分布N(2, )(
)( >0).若
>0).若 在(
在( ,1)内取值的概率为0.15,则
,1)内取值的概率为0.15,则 在(2,3)内取值的概率为0.7;
在(2,3)内取值的概率为0.7;
④若双曲线 的渐近线方程为
的渐近线方程为 ,则k=1.其中正确命题的序号是.
,则k=1.其中正确命题的序号是.
已知直线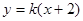 (k>0)与抛物线
(k>0)与抛物线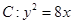 相交于
相交于 、
、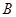 两点,
两点,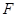 为
为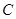 的焦点,若
的焦点,若 ,则k的值为.
,则k的值为.
等差数列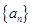 满足:
满足: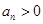 ,且前
,且前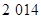 项和
项和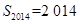 ,则
,则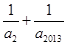 的最小值为________.
的最小值为________.
已知实数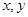 满足:
满足: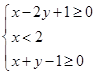 ,则
,则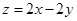 的最大值为.
的最大值为.
在平面直角坐标系中,点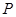 是由不等式组
是由不等式组 所确定的平面区域内的动点,
所确定的平面区域内的动点, 是直线
是直线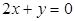 上任意一点,
上任意一点,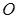 为坐标原点,则
为坐标原点,则 的最小值为.
的最小值为.