甲和乙两个几何体都是由大小相同的小立方块搭成,它们的俯视图如图,小正方形中数字表示该位置上的小立方块个数,则下列说法中正确的是

| A. |
甲和乙左视图相同,主视图相同 |
| B. |
甲和乙左视图不相同,主视图不相同 |
| C. |
甲和乙左视图相同,主视图不相同 |
| D. |
甲和乙左视图不相同,主视图相同 |
如图矩形ABCD中,折叠矩形一边AD,使点D落在BC边的点F处,已知折痕AE=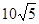 cm,且CE:CF=3:4,则矩形ABCD的周长为()
cm,且CE:CF=3:4,则矩形ABCD的周长为()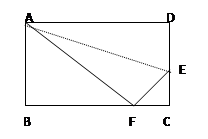
| A.36cm | B.36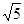 cm cm |
C.72cm | D.72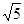 cm cm |
如图,O为△ABC中线的交点,则 的值为()
的值为()
A. |
B.2 | C.3 | D.4 |
如图,AD是△ABC高线,DE AB于E, DF
AB于E, DF AC于F,则
AC于F,则 中正确的有()
中正确的有()
| A.1个 | B.2 个 | C.3个 | D.4个 |
如图,BD AC,CE
AC,CE AB,BD、CE交于点O,那么图形中相似的三角形共有 ()
AB,BD、CE交于点O,那么图形中相似的三角形共有 ()
A.2对 B.4对 C.5对 D.6对
在△ABC和△A′B′C′中,如果AB="9,BC=8,AC=5," A′B′= , B′C′=
, B′C′= ,A′C′=4,那么 ()
,A′C′=4,那么 ()
| A.∠A=∠A′ | B.∠B=∠A′ | C.∠A=∠C′ | D.不能确定 |