如图,一次函数 的图象与反比例函数 的图象交于点 、 ,与 轴交于点 ,若 ,且 .
(1)求反比例函数与一次函数的表达式;
(2)请直接写出不等式 的解集.

观察下表:
| 列举 |
猜想 |
| 3,4,5 |
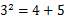 |
| 5,12,13 |
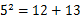 |
| 7,24,25 |
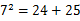 |
| … … |
… … |
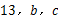 |
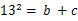 |
请你结合该表格及相关知识,求出 的值.
的值.
如图,台风过后,一希望小学的旗杆在离地某处断裂,旗杆顶部落在离旗杆底部8m处,已知旗杆原长16 m,你能求出旗杆在离底部多少米的位置断裂吗?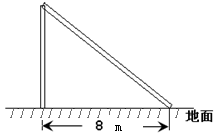
若三角形的三个内角的比是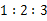 ,最短边长为1,最长边长为2.
,最短边长为1,最长边长为2.
求:(1)这个三角形各内角的度数;
(2)另外一条边长的平方.
在△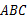 中,
中, ,
,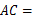
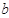 ,
,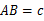 .若
.若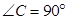 ,如图①,根据勾股定理,则
,如图①,根据勾股定理,则 .若△
.若△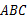 不是直角三角形,如图②和图③,请你类比勾股定理,试猜想
不是直角三角形,如图②和图③,请你类比勾股定理,试猜想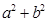 与
与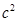 的关系,并证明你的结论.
的关系,并证明你的结论.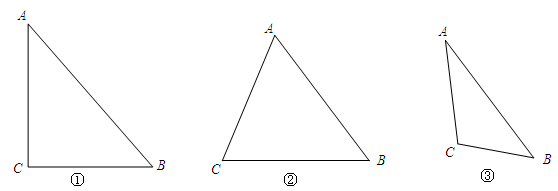
若△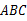 三边长满足下列条件,判断△
三边长满足下列条件,判断△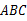 是不是直角三角形,若是,请说明哪个角是直角.
是不是直角三角形,若是,请说明哪个角是直角.
(1)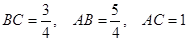 ;
;
(2)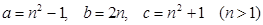 .
.