已知函数 , 则该函数 (
| A. |
奇函数, 最大值为 2 |
B. |
偶函数,最大值为 2 |
| C. |
奇函数, 最大值为 |
D. |
偶函数, 最大值为 |
若 ,
, 且
且 ,则在
,则在 ,
,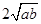 ,
, 和
和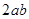 中最大的是()
中最大的是()
A. |
B.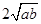 |
C. |
D.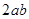 |
若 是不全相等的实数,求证:
是不全相等的实数,求证: .
.
证明过程如下: ,
,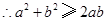 ,
, ,
, ,
,
又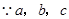 不全相等,
不全相等, 以上三式至少有一个“
以上三式至少有一个“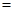 ”不成立,
”不成立, 将以上三式相加得
将以上三式相加得 ,
, .
.
此证法是()
| A.分析法 | B.综合法 | C.分析法与综合法并用 | D.反证法 |
使不等式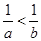 成立的条件是()
成立的条件是()
A.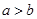 |
B.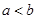 |
C.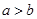 且 且 |
D.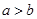 且 且 |
用反证法证明“如果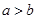 ,则
,则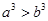 ”假设的内容是()
”假设的内容是()
A. |
B.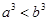 |
C. 且 且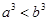 |
D. 或 或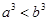 |
用反证法证明一个命题时,下列说法正确的是()
| A.将结论与条件同时否定,推出矛盾 |
| B.肯定条件,否定结论,推出矛盾 |
| C.将被否定的结论当条件,经过推理得出结论只与原题条件矛盾,才是反证支的正确运用 |
| D.将被否定的结论当条件,原题的条件不能当条件 |