在新冠肺炎疫情防控期间,某超市开通网上销售业务,每天能完成1200份订单的配货,由于订单量大幅增加,导致订单积压.为解决困难,许多志愿者踊跃报名参加配货工作.已知该超市某日积压500份订单未配货,预计第二天的新订单超过1600份的概率为0.05,志愿者每人每天能完成50份订单的配货,为使第二天完成积压订单及当日订单的配货的概率不小于0.95,则至少需要志愿者( )
| A. |
10名 |
B. |
18名 |
C. |
24名 |
D. |
32名 |
函数y=x+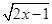 ( )
( )
A.有最小值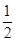 ,无最大值 ,无最大值 |
B.有最大值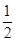 ,无最小值 ,无最小值 |
C.有最小值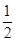 ,最大值2 ,最大值2 |
| D.无最大值,也无最小值 |
若函数f(x)=x2+2(a-1)x+2在区间(-∞,4)上是减函数,则实数a的取值范围是( )
| A.a≤-3 | B.a≥-3 |
| C.a≤5 | D.a≥3 |
已知函数f(x)在(-∞,+∞)上是增函数,a,b∈R,且a+b>0,则有( )
| A.f(a)+f(b)>-f(a)-f(b) |
| B.f(a)+f(b)<-f(a)-f(b) |
| C.f(a)+f(b)>f(-a)+f(-b) |
| D.f(a)+f(b)<f(-a)+f(-b) |
如果函数f(x)在[a,b]上是增函数,对于任意的x1、x2∈[a,b](x1≠x2),则下列结论中不正确的是( )
A.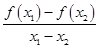 >0 >0 |
| B.(x1-x2)[f(x1)-f(x2)]>0 |
| C.f(a)<f(x1)<f(x2)<f(b) |
D.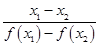 >0 >0 |
函数y=x2-6x+10在区间(2,4)上是( )
| A.递减函数 | B.递增函数 |
| C.先递减再递增 | D.先递增再递减 |