在 中, ,再从条件①、条件②这两个条件中选择一个作为己知,求:
(Ⅰ)a的值:
(Ⅱ) 和 的面积.
条件①: ;
条件②: .
注:如果选择条件①和条件②分别解答,按第一个解答计分.
(本小题满分12分)设函数 在
在 时取得极值.
时取得极值.
(Ⅰ)求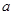 的值;
的值;
(Ⅱ)求函数 的单调区间.
的单调区间.
已知椭圆C: 的离心率为
的离心率为 ,
, 是椭圆的两个焦点,P是椭圆上任意一点,且
是椭圆的两个焦点,P是椭圆上任意一点,且 的周长是
的周长是
(1)求椭圆C的方程;
(2)设圆T: ,过椭圆的上顶点作圆T的两条切线交椭圆于
,过椭圆的上顶点作圆T的两条切线交椭圆于 两点,当圆心在
两点,当圆心在 轴上移动且
轴上移动且 时,求
时,求 的斜率的取值范围.
的斜率的取值范围.
若函数 是定义域D内的某个区间
是定义域D内的某个区间 上的增函数,且
上的增函数,且 在
在 上是减函数,则称
上是减函数,则称 是
是 上的“单反减函数”,已知
上的“单反减函数”,已知
(1)判断 在
在 上是否是“单反减函数”;
上是否是“单反减函数”;
(2)若 是
是 上的“单反减函数”,求实数
上的“单反减函数”,求实数 的取值范围.
的取值范围.
如图,在四棱锥 中,
中, 底面
底面 ,底面
,底面 是梯形,其中
是梯形,其中 ,
, ,
, 与
与 交于点
交于点 ,
, 是
是 边上的点,且
边上的点,且 ,已知
,已知 ,
, ,
, .
.
(1)求平面 与平面
与平面 所成锐二面角的正切;
所成锐二面角的正切;
(2)已知 是
是 上一点,且
上一点,且 平面
平面 ,求
,求 的值.
的值.
已知等差数列 满足
满足 、
、 、
、 成等比数列,数列
成等比数列,数列 的前
的前 项和
项和 (其中
(其中 为正常数)
为正常数)
(1)求 的前项和
的前项和 ;
;
(2)已知 ,
, ,求
,求