日晷是中国古代用来测定时间的仪器,利用与晷面垂直的晷针投射到晷面的影子来测定时间.把地球看成一个球(球心记为 O),地球上一点 A的纬度是指 OA与地球赤道所在平面所成角,点 A处的水平面是指过点 A且与 OA垂直的平面.在点 A处放置一个日晷,若晷面与赤道所在平面平行,点 A处的纬度为北纬40°,则晷针与点 A处的水平面所成角为( )

| A. |
20° |
B. |
40° |
| C. |
50° |
D. |
90° |
函数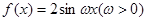 在区间
在区间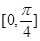 上单调递增,且在这个区间上的最大值是
上单调递增,且在这个区间上的最大值是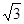 ,那么
,那么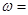
A.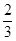 |
B.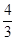 |
C.2 | D.4 |
函数 满足
满足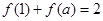 ,则
,则 的所有可能值为
的所有可能值为
A.1或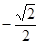 |
B.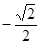 |
C.1 | D.1或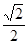 |
如图,取一个底面半径和高都为R的圆柱,从圆柱中挖去一个以圆柱的上底面为底面,下底面圆心为顶点的圆锥,把所得的几何体与一个半径为R的半球放在同一水平面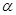 上.用一平行于平面
上.用一平行于平面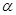 的平面去截这两个几何体,截面分别为圆面和圆环面(图中阴影部分).设截面面积分别为
的平面去截这两个几何体,截面分别为圆面和圆环面(图中阴影部分).设截面面积分别为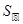 和
和 ,那么
,那么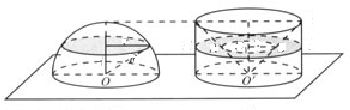
A.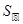 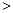  |
B.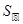 = = |
C.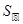 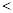  |
D.不确定 |
已知正方形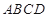 的边长为
的边长为 ,
, 为
为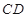 的中点,
的中点, 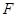 为
为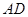 的中点,则
的中点,则
| A.0 | B.1 | C.2 | D.4 |
根据如下样本数据
| x |
3 |
4 |
5 |
6 |
7 |
| y |
4.0 |
2.5 |
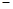 0.5 0.5 |
0.5 |
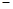 2.0 2.0 |
得到的回归方程为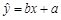 .若
.若 ,则
,则 的值为
的值为
A. B.
B. C.
C.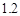 D.
D.