Logistic模型是常用数学模型之一，可应用于流行病学领城．有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数 I( t)( t的单位：天)的 Logistic模型： ，其中 K为最大确诊病例数．当 I( )=0.95 K时，标志着已初步遏制疫情，则 约为（ ）（ln19≈3）
| A． |
60 |
B． |
63 |
C． |
66 |
D． |
69 |
设非零向量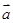
、
、
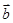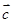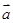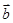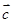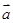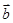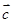、满足||=||=||，+=，则向量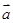、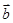间的夹角为（）
| A．150° | B．120° | C．60° | D．30° |
已知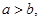
函数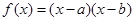
的图象如右图所示，则函数
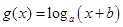的图象可能为 ( )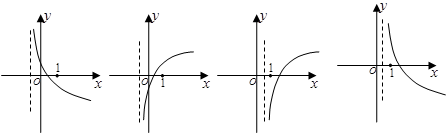
|
|
|
|
||||||||
下列说法：
①将一组数据中的每个数据都加上或减去同一个常数后，方差恒不变；
②设有一个回归方程
，变量
增加一个单位时，
平均增加5个单位；
③线性回归方程
必过
；
④在一个
列联表中，由计算得K2=13.079，则有99%的把握确认这两个变量间有关系；其中错误的个数是
| A．0 | B．1 | C．2 | D．3 |
本题可以参考独立性检验临界值表
 |
0.5 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.535 |
7.879 |
10.828 |
已知数列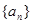
满足a1=1,且
=
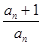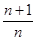，则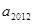
=（）
| A．2010 | B．2011 | C．2012 | D．2013 |
从集合{1，2，3，4，5}中随机抽取一个数为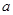
，从集合{1，2，3}中随机抽取一个数为
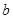，则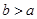
的概率是( )
A． |
B． |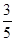
C． |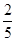
D． |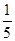
