若函数 ,则下列结论正确的是( )
| A. |
, 在 上是增函数 |
| B. |
, 在 上是减函数 |
| C. |
是偶函数 |
| D. |
是奇函数 |
【2015高考山东,理6】已知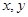 满足约束条件
满足约束条件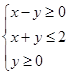 ,若
,若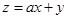 的最大值为4,则
的最大值为4,则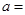 ()
()
| A.3 | B.2 | C.-2 | D.-3 |
【2015高考福建,理5】若变量 满足约束条件
满足约束条件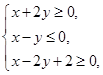 则
则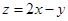 的最小值等于 ()
的最小值等于 ()
A. |
B.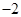 |
C.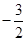 |
D.2 |
【2015高考山东,理5】不等式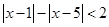 的解集是()
的解集是()
A.(-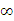 ,4) ,4) |
B.(-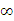 ,1) ,1) |
C.(1,4) | D.(1,5) |
【2015高考陕西,理10】某企业生产甲、乙两种产品均需用A,B两种原料.已知生产1吨每种产品需原料及每天原料的可用限额如表所示,如果生产1吨甲、乙产品可获利润分别为3万元、4万元,则该企业每天可获得最大利润为()
| 甲 |
乙 |
原料限额 |
|
 (吨) (吨) |
 |
 |
 |
 (吨) (吨) |
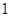 |
 |
 |
A.12万元 B.16万元 C.17万元 D.18万元
【2015高考天津,理2】设变量 满足约束条件
满足约束条件 ,则目标函数
,则目标函数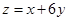 的最大值为()
的最大值为()
| A.3 | B.4 | C.18 | D.40 |