已知函数 .
(1)求 的定义域与最小正周期;
(2)讨论f(x)在区间 上的单调性.
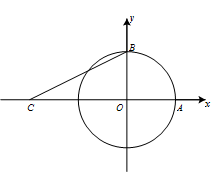
(本小题满分14分)如图,曲线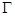 :
: 分别与
分别与 、
、 轴的正半轴交于点
轴的正半轴交于点 、
、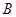 ,点
,点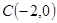 ,角
,角 、
、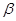 的终边分别与曲线
的终边分别与曲线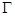 交于点
交于点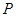 、
、 .
.
(Ⅰ)若 与
与 共线,求
共线,求 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,若 ,求
,求 在
在 方向上的投影;
方向上的投影;
(Ⅲ)有研究性小组发现:若满足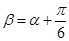 ,则
,则 是一个定值,你认为呢?若是,请求出定值,若不是,请说明理由.
是一个定值,你认为呢?若是,请求出定值,若不是,请说明理由.
(本小题满分12分).已知向量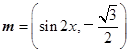 ,
,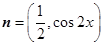 ,函数
,函数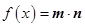 .
.
(Ⅰ)试用五点作图法画出函数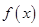 在一个周期内的图象(要求列表);
在一个周期内的图象(要求列表);
(Ⅱ)求方程 在
在 内的所有实数根之和.
内的所有实数根之和.
(本小题满分12分)函数 部分图象如图所示,其中
部分图象如图所示,其中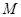 、
、 、
、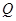 分别是函数图象在
分别是函数图象在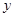 轴右侧的第一、二个零点、第一个最低点,且
轴右侧的第一、二个零点、第一个最低点,且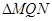 是等边三角形.
是等边三角形.
(Ⅰ)求函数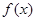 的解析式;
的解析式;
(Ⅱ)若 ,求
,求 的值.
的值.
(本小题满分12分)已知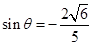 ,
, .
.
(Ⅰ)求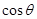 ,
,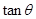 的值;
的值;
(Ⅱ)求 的值.
的值.
(本小题满分12分)在 中,已知
中,已知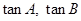 是
是 的方程
的方程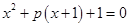 的两个根.
的两个根.
(Ⅰ)求 ;
;
(Ⅱ)若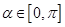 ,且满足
,且满足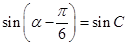 ,求
,求 的值.
的值.