设函数 在 ,内有定义。对于给定的正数K,定义函数 取函数 。若对任意的 ,恒有 ,则 ( )
| A. |
K的最大值为2 |
B. |
K的最小值为2 |
| C. |
K的最大值为1 |
D. |
K的最小值为1 |
在数列{an}中,an+1=can(c为非零常数),前n项和为Sn=3n+k,则实数k的值为( )
| A.-1 | B.0 |
| C.1 | D.2 |
若a+bi=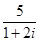 (i是虚数单位,a,b∈R),则ab=( )
(i是虚数单位,a,b∈R),则ab=( )
| A.-2 | B.-1 |
| C.1 | D.2 |
已知抛物线x2=4y上有一条长为6的动弦AB,则AB的中点到x轴的最短距离为( )
A.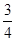 |
B.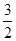 |
| C.1 | D.2 |
已知F1,F2分别是双曲线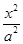 -
-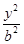 =1(a>0,b>0)的左、右焦点,P为双曲线右支上的任意一点.若
=1(a>0,b>0)的左、右焦点,P为双曲线右支上的任意一点.若 =8a,则双曲线的离心率的取值范围是( )
=8a,则双曲线的离心率的取值范围是( )
| A.(1,2] | B.[2,+∞) |
| C.(1,3] | D.[3,+∞) |
已知椭圆 +
+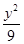 =1及以下3个函数:①f(x)=x;②f(x)=sin x;③f(x)=cos x.其中函数图像能等分该椭圆面积的函数个数有( )
=1及以下3个函数:①f(x)=x;②f(x)=sin x;③f(x)=cos x.其中函数图像能等分该椭圆面积的函数个数有( )
| A.1个 | B.2个 |
| C.3个 | D.0个 |