给定无穷数列 ,若无穷数列{b n}满足:对任意 ,都有 ,则称 "接近"。
(1)设 是首项为1,公比为 的等比数列, , ,判断数列 是否与 接近,并说明理由;
(2)设数列 的前四项为: =1, =2, =4, =8, 是一个与 接近的数列,记集合M={x|x=b i, i=1,2,3,4},求M中元素的个数m;
(3)已知 是公差为d的等差数列,若存在数列{b n}满足:{b n}与 接近,且在b₂-b₁,b₃-b₂,…b 201-b 200中至少有100个为正数,求d的取值范围。
已知抛物线 过点
过点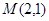 .
.
(I)求抛物线的方程;
(II)已知圆心在 轴上的圆
轴上的圆 过点
过点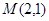 ,且圆
,且圆 在点
在点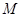 的切线恰是抛物线在点
的切线恰是抛物线在点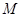 的切线,求圆
的切线,求圆 的方程;
的方程;
(Ⅲ)如图,点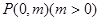 为
为 轴上一点,点
轴上一点,点 是点
是点 关于原点的对称点,过点
关于原点的对称点,过点 作一条直线与抛物线交于
作一条直线与抛物线交于 两点,若
两点,若 ,证明:
,证明: .
.
小王需不定期地在某超市购买同一品种的大米.现有甲、乙两种不同的采购策略,策略甲:每次购买大米的数量一定;策略乙:每次购买大米的钱数一定.若以 (元)和
(元)和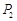 (元)分别记小王先后两次买米时,该品种大米的单价,请问:仅这两次买米而言,甲、乙两种购买方式,从平均单价考虑,哪种比较合算?请进行探讨,并给出探讨过程.
(元)分别记小王先后两次买米时,该品种大米的单价,请问:仅这两次买米而言,甲、乙两种购买方式,从平均单价考虑,哪种比较合算?请进行探讨,并给出探讨过程.
几何体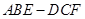 的三视图如图,
的三视图如图, 与
与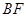 交于点
交于点 ,
,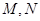 分别是直线
分别是直线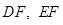 的中点,
的中点,
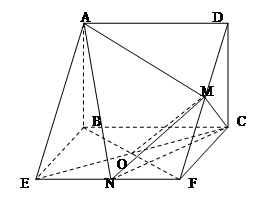
(I) 面
面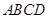 ;
;
(II)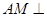 面
面 ;
;
(Ⅲ)求二面角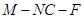 的平面角的余弦值.
的平面角的余弦值.
已知函数 (
(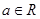 )在
)在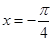 取到极值,
取到极值,
(I)写出函数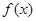 的解析式;
的解析式;
(II)若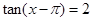 ,求
,求 的值;
的值;
(Ⅲ)从区间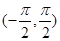 上的任取一个
上的任取一个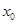 ,若
,若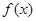 在点
在点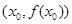 处的切线的斜率为
处的切线的斜率为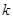 ,求
,求 的概率.
的概率.
已知椭圆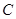 :
: (
( )的短轴长与焦距相等,且过定点
)的短轴长与焦距相等,且过定点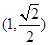 ,倾斜角为
,倾斜角为 的直线
的直线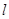 交椭圆
交椭圆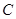 于
于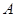 、
、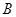 两点.
两点.
(Ⅰ)求椭圆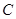 的方程;
的方程;
(Ⅱ)确定直线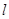 在
在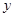 轴上截距的范围.
轴上截距的范围.