设函数
,
,其中
,
.若
,
,且
的最小正周期大于
,则( )
A. , B. , C. , D. ,
从正方体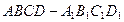 的8个顶点中选取4个作为四面体的顶点,可得到的不同四面体的个数为( )
的8个顶点中选取4个作为四面体的顶点,可得到的不同四面体的个数为( )
A.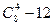 |
B.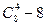 |
C.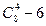 |
D. |
某学生要邀请10位同学中的6位参加一项活动,其中有2位同学不能同时参加,则邀请的方法有( )种
| A.84 | B.98 | C.112 | D.140 |
有11名学生,其中女生3名,男生8名,从中选出5名学生组成代表队,要求至少有1名女生参加,则不同的选派方法种数是( )
| A.406 | B.560 | C.462 | D.154 |
平面上有5个点,其中任何3个点都不共线,那么可以连成的三角形的个数是( )
| A.3 | B.5 | C.10 | D.20 |
甲、乙、丙三地之间有直达的火车,相互之间的距离均不相等,且无通票,问车票票价的种数是( )
| A.1 | B.2 | C.3 | D.6 |