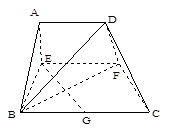在平面直角坐标系xOy中,设点集
,
令 .从集合 M n中任取两个不同的点,用随机变量 X表示它们之间的距离.
(1)当 n=1时,求 X的概率分布;
(2)对给定的正整数 n( n≥3),求概率 P( X≤ n)(用 n表示).
(本小题满分12分) 已知函数 (
(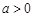 且
且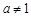 )的图象过点
)的图象过点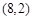 ,点
,点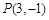 关于直线
关于直线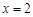 的对称点
的对称点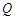 在
在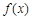 的图象上.
的图象上.
(Ⅰ)求函数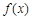 的解析式;
的解析式;
(Ⅱ)令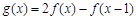 ,求
,求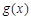 的最小值及取得最小值时x的值.
的最小值及取得最小值时x的值.
(本小题满分12分) 在△ABC中,a、b、c分别为内角A、B、C的对边,且满足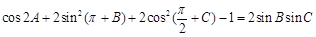 .
.
(Ⅰ)求角A的大小;
(Ⅱ)若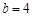 、
、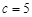 ,求
,求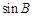 .
.
(本小题满分12分) 命题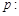 实数x满足
实数x满足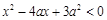 (其中
(其中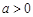 ),命题
),命题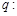 实数
实数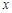 满足
满足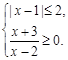
(Ⅰ)若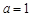 ,且
,且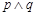 为真,求实数
为真,求实数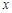 的取值范围;
的取值范围;
(Ⅱ)若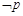 是
是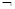
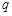 的充分不必要条件,求实数a的取值范围.
的充分不必要条件,求实数a的取值范围.
(本小题满分12分) 已知等差数列 的前n项和为
的前n项和为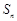 ,且
,且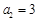 ,
,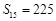 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设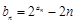 ,求数列
,求数列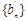 的前n项和
的前n项和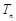 .
.
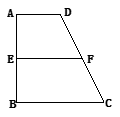
(本小题满分14分)已知梯形ABCD中,AD∥BC,∠ABC =∠BAD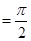 ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE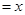 ,G是BC的中点.沿EF将梯形ABCD翻折,
,G是BC的中点.沿EF将梯形ABCD翻折,
使平面AEFD⊥平面EBCF (如图).
(1)当 时,求证:BD⊥EG ;
时,求证:BD⊥EG ;
(2)若以F、B、C、D为顶点的三棱锥的体积记为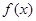 ,求
,求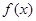 的最大值;
的最大值;
(3)当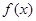 取得最大值时,求二面角D-BF-C的余弦值.
取得最大值时,求二面角D-BF-C的余弦值.